Съюзан Кодиш - Верните себе здравомыслие - Применяя нестандартный подход общей семантики

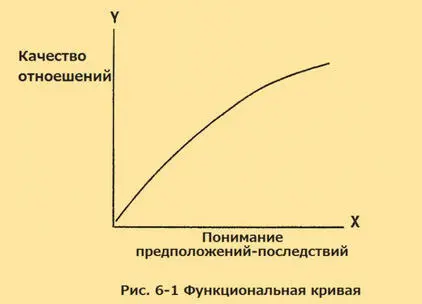
На горизонтальную линию, называемую ось « x », мы помещаем «понимание предположений-последствий». На вертикальную линию, называемую ось « y », мы помещаем «качество отношений». Для каждого значения « x », отмеченного на горизонтальной линии, мы можем найти соответствующее значения « y » на вертикальной линии. Затем мы можем отметить точки на графике, где два значения пересекаются. Таким образом, мы показываем, что когда меняется одно, меняется и другое. Когда увеличивается значение «понимание предположений-последствий», увеличивается и «качество отношений».

Уэнделл Джонсон называл функциональную кривую «символом науки», когда писал: «универсальный символ науки и научного образа жизни… Она представляет то, что любой учёный стремится выразить: изменение одного рода, изменение другого рода, и отношения между ними». 45

Функциональные отношения, выраженные такой кривой, также помогают нам делать более точные прогнозы. Когда мы можем описать (присвоить значение) одному фактору, мы можем определить значения факторов, к которым он функционально относится.

Вы можете начать искать функции и переменные в ситуациях, с которыми вы имеете дело каждый день. Некоторые функции, которые мы замечаем в нашей работе с людьми, включают следующие. Боль в спине может быть функцией привычек движения и поддержания осанки, типов кресел в которых они сидят, определённого состояния их мышц и суставов, уровня тревоги, и т. д. ‘Эмоциональное’ состояние людей может быть функцией того, как они говорят сами с собой, типов их межличностных отношений, их целей на будущее, истории их семьи, количество кофеина, которое они потребляют, и т. д.

Заметьте, что определённое ‘следствие’, как боль в спине или ‘эмоциональное’ недомогание, скорее всего, будут функцией многих переменных, которые обычно называют ‘причинами’. Определённое ‘следствие’ может также служить ‘причиной’. Например, боль в спине может функционировать как причина ‘эмоционального’ недомогания.

Бывает и наоборот, когда определённая ‘причина’ служит переменной в нескольких различных функциях с множеством следствий. Например, то, что вы скажете, может быть интерпретировано по-разному, в зависимости от слушателей, их ожиданий, и т. д. То, что вы делаете, может произвести несколько различных эффектов, за гранью ваших ожидаемых последствий. Когда вы имеете дело с какой-либо сложной системой или комплексом отношений, полезно вспомнить слова Гарретта Хардина, которые он сам назвал первым законом экологии: «Вы никогда не можете делать лишь что-то одно». 46

Любое функциональное отношение, которое мы замечаем, составляет карту, которую мы создали. Поэтому, полезным и даже обязательным будет помнить о том, что это не территория. Её стоит исследовать, проверять и отклонять или модифицировать по необходимости.

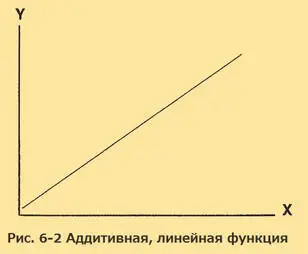
Некоторые отношения происходят относительно просто и прямо. Например, представьте, что вы пригласили близкого друга на десерт, а к вашему порогу неожиданно прибыло ещё четыре человека. Накрывая на стол, вы можете добавить одну тарелку и одну кружку для каждого нового человека. Таким образом, мы можем сказать, что для каждого нового человека (независимая переменная) вы добавляете два предмета из сервиза (зависимая переменная). Такое отношение называется аддитивным.

Примером аддитивных отношений может быть функция y=f( 2 x) . Значение y увеличивается аддитивно, на 2 раза, по мере того, как x увеличивается на 1. Таким образом, у нас получается 2, 4, 6, 8, 10, и т. д. Каждое последующее значение y получается за счёт сложения предыдущего значения y с заданным количеством (в этом случае с 2). Такое отношение также называется линейным, потому что его график (кривая) выглядит как прямая линия (рис. 6–2).

Мы можем сравнить это с не-аддитивными отношениями, примером которых может служить функция y=f( 2 x) . Значение y увеличивается не-аддитивно; и так у нас получается 2, 4, 8, 16, 32, и т. д. Каждое последующее значение y получается путём умножения предшествующего значения y на заданное число (в этом случае на 2). Это отношение называется нелинейным, потому что его кривая, нарисованная на графике, имеет изменяющийся, а не прямой наклон (рис. 6–3).