Умберто Эко - Роль читателя. Исследования по семиотике текста [litres]

Когда Хинтикка (Hintikka, 1969b) говорит: если я вижу человека, не будучи уверен, Джон ли это, или Генри, или кто-то совсем другой, то все равно этот человек будет тем же самым в любом возможном мире, потому что это человек, которого я вижу в этот конкретный момент, – тем самым Хинтикка формулирует в терминах восприятия ту же проблему текстового топика, о которой я здесь веду речь. Поскольку мой вопрос формулируется так: «Кто этот человек, которого я вижу в данный момент?» – то единственное существенное свойство этого индивида состоит в том, что он видим мною. Мои материальные и эмпирические потребности определяют то, что значимо в данном (кон)тексте.

Теперь мы попытаемся определить, в каком смысле можно говорить о доступности одного мира по отношению к другому.

Согласно имеющейся литературе по данной проблематике доступность – это бинарное отношение W i RW j , где W j доступен для W i . Если мы хотим избежать психологизирующей интерпретации термина доступность (например: «индивид в мире W i может “представить себе” мир W j »), то мы должны сказать примерно вот что: W j доступен для W i , если мироструктура W i может порождать – посредством манипуляций отношениями между индивидами и свойствами – мироструктуру W j .

Отношения между мирами могут быть разными:

a) W i RW j , но не W j RW i : отношение бинарное, но не симметричное;

b) W i RW j и W j RW i : отношение бинарное и симметричное;

c) W i RW j , W j RW k , W i RW k : отношение бинарное и транзитивное;

d) предыдущее отношение – но к тому же и симметричное.

Если имеется два или большее число миров, то вышеобозначенные отношения могут изменяться в зависимости от следующих обстоятельств:

α) число индивидов и свойств одинаково во всех мирах;

β) число индивидов и свойств увеличивается по крайней мере в одном мире;

γ) число индивидов и свойств уменьшается по крайней мере в одном мире;

δ) свойства изменяются;

ε) (прочие возможные варианты, возникающие из комбинаций вышеназванных условий).

Что касается миров нарративных (воображаемых), то на данной основе можно было бы попытаться разработать типологию различных литературных жанров (см. интересные наметки Т. Павела – Pavel, 1975). Здесь мы рассмотрим лишь несколько примеров, интересных для нашей темы. Для начала возьмем пример с двумя мирами, имеющими одинаковое число индивидов и одинаковое число одинаковых свойств (не будем пока различать свойства существенные и случайные, «акцидентные»):

Рис. 8.11

Очевидно, что посредством некоторых комбинаторных манипуляций индивиды в мире W 1можно сделать структурно подобными индивидам в мире W 2 – и наоборот. Следовательно, отношение между мирами здесь бинарное и симметричное (W 1RW 2и W 2RW 1).

Рассмотрим теперь другой пример: в мире W 1имеется меньше свойств, чем в мире W 2. Представим себе (вслед за Хинтиккой – см. выше раздел 8.4.3), что в мире W 1есть свойства «круглый» и «красный», а в мире W 2индивид может иметь еще одно свойство: «крутящийся».

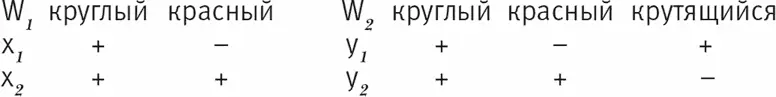
Рис. 8.12

Можно сказать, что в мире W 2 нетрудно породить индивиды из мира W 1 : достаточно в колонке «крутящийся» проставить минус (т. е. придать индивиду свойство «некрутящийся»):

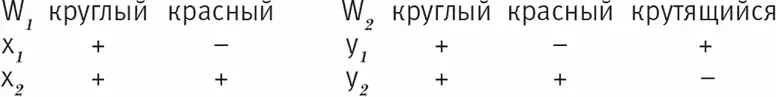
Рис. 8.13

Произведя такую операцию, мы видим, что y 4 структурно идентичен у 2 , в то время как y 3 – это совершенно новый индивид (который прежде в W 2 не существовал, но был потенциально представим).

Столь же очевидно, что невозможно проделать подобную операцию в мире W 1 , по отношению к миру W 2 : W 1 имеет более бедную матрицу (или мироструктуру), которая не может учесть наличие или отсутствие свойства «крутящийся». Стало быть, отношение между мирами W 1 и W 2 – несимметрично (W 2 R W 1 , но не W 1 RW 2 ). В рамках второго мира можно «вообразить», «представить себе» (т. е. воссоздать в силу гибкости его структуры) мир первый, но не наоборот. Подобная ситуация описана Э. Э. Эбботом [500]в его «Флатландии». Существо из трехмерного мира попадает в мир, где всего два измерения: гость может понять и описать мир, в котором он очутился, но обитатели этого мира не в состоянии даже представить себе своего гостя. Гость может проходить сквозь этот мир, обитатели которого мыслят лишь в терминах плоских фигур. Шар, имеющий три измерения, проходя через двухмерный мир, представляется в нем как ряд окружностей различного размера, но существа из этого мира не могут понять, почему пришелец постоянно меняет свой размер.