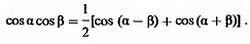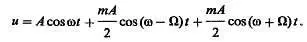Владимир Поляков - Посвящение в радиоэлектронику

Мы узнали, что спектр синусоидального колебания самый простой: он состоит всего из одной спектральной линии на «своей» частоте f 0. Вот почему несущие колебания радиовещательных станций строго синусоидальны. Нельзя же допустить, чтобы одна и та же станция принималась одновременно на нескольких частотах! После такого заключения некоторые из наиболее любознательных читателей могут прийти к полному недоумению: при передаче сигналов по радио надо применять синусоидальное несущее колебание, которое никакой информации не несет! Но информация-то все-таки передается! Никакого противоречия здесь, разумеется, нет. Прежде всего надо заметить, что исходный сигнал, несущий информацию (телеграфный, речевой или музыкальный), занимает некоторый спектр частот. Мы уже говорили о его ширине, а теперь изобразим сигнал и спектр графически. Обратите внимание, что спектр теперь уже не линейчатый, а сплошной. Линейчатым спектром обладают только периодические процессы, регулярно повторяющиеся во времени. А передача информации — процесс случайный, вероятностный. В зависимости от текста телеграммы могут передаваться различные сочетания точек и тире. И им будут соответствовать различные спектры.

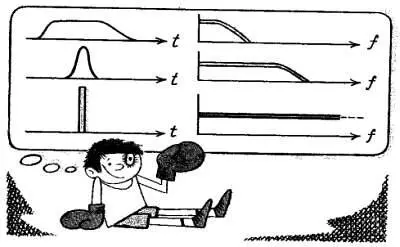
Импульсы и их спектры.

Но общей для них будет занимаемая полоса частот, указанная на графиках. Ширина ее обозначена буквой В . Наложим передаваемый сигнал на синусоидальную несущую. Излучаемый в эфир или передаваемый по линии модулированный сигнал уже не будет чисто синусоидальным: его амплитуда будет изменяться в такт с передаваемым сообщением. Спектр излучаемого сигнала станет таким, как показано на рисунке. Кроме спектральной линии на частоте f 0— несущей — появятся боковые полосы. Это два зеркально-симметричных спектра по обе стороны от несущей. Форма их при амплитудной модуляции точно повторяет форму спектра исходного сигнала.

Спектр белого света.

Сигналы и их спектры.

Образование двух боковых полос в спектре AM колебания можно пояснить математически. Только удобнее вместо синусов взять четные функции косинусы (выражения при этом получаются проще и понятнее). А форма косинусоидального колебания точно такая же, как и синусоидального. Пусть несущая A· cos ωtпромодулирована по амплитуде низкочастотным косинусоидальным колебанием с угловой частотой Ω. Вид получившегося сигнала показан на рисунке. Его максимальная амплитуда равна (1 + m) А, а минимальная - (1 — m) А. Параметр mназывается коэффициентом модуляции .

При AM он не может быть больше единицы, поскольку уже при m= 1 минимальная амплитуда сигнала падает до нуля. Запишем выражение для AM сигнала:

u = А(1 + m·cos Ωt)·cos ωt,

где А— амплитуда несущей; ω— угловая частота несущей; Ω— угловая частота модулирующего колебания.

Это выражение легко преобразовать с помощью известного тригонометрического тождества

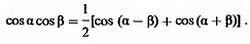
Раскрывая скобки и используя это тождество, получаем

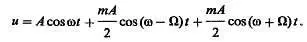
Из этого выражения видно, что напряжение сигнала является суммой трех синусоидальных колебаний; несущей (первое слагаемое), нижней боковой частоты (второе слагаемое) и верхней боковой частоты (третье слагаемое). Эти три колебания и составляют спектр сигнала при AM синусоидальным сигналом. Если же в модулирующем сигнале содержится несколько низкочастотных ко-

…

засада:( В источнике OCR отсутствуют стр. 52, 53

…

И устройство, вполне пригодное для этой цели, нам уже встречалось. Вспомните простейший датчик углового положения фюзеляжа самолета. Если жесткий отвес с грузом на конце заставить колебаться подобно маятнику, то с движка потенциометра можно будет снять синусоидальный электрический сигнал. Есть только два существенных «но», из-за которых подобные устройства не нашли практического применения.

Преобразователь колебаний маятника в электрический сигнал.

Первое «но» — частота генерируемых колебаний оказывается слишком низкой. Сколько раз в секунду может качнуться маятник?