Формирование взаимоотображений системы и среды связано, в первую очередь, с определением границы системы. Нетривиальность этой процедуры определяется во многом неопределенностью самого фундаментального понятия «система». Например, в классическом определении динамической системы ее атрибутом является множество допустимых входных воздействий, но ведь это атрибут внешней среды. Точно так же понятие границы системы размывается при попытке ее определения через понятие эффективности, что приводит к необходимости рассмотрения структуры метасистемы, которая, в свою очередь, порождает следующий цикл неопределенности.
В реальных условиях можно считать, что имеется некоторое идентифицирующее свойство, позволяющее выделять систему S из окружающей среды. Назовем это свойство границей системы . Сейчас речь не идет о самом правиле выбора этого свойства. Главное, что такое свойство является фундаментальным феноменологическим атрибутом системы. По-видимому, здесь проявляются некоторые аналогии эксклюзивности понятий фундаментальных абстрактных категорий, к которым, несомненно, относится и понятие «система». Некоторая близость проблемы дефиниции в этом случае, на наш взгляд, возможно, наблюдается с развитием такого фундаментального понятия математики, как множество в некоторый новый уровень абстракции, представленной в математической «Теории категорий».
Приведем в этом плане некоторые выдержки из замечательного учебника «Основы теории категорий» отечественных математиков М.Цаленко, и Е.Шульгейфера из Московского государственного университета. « Характерной чертой современной математики является изучение математических объектов вместе с отображениями этих объектов друг в друга, согласованными со структурой объектов: теория множеств немыслима без отображения множеств, топология немыслима без непрерывных отображений, алгебра немыслима без гомоморфизмов алгебраических систем и т.д. Обычно объекты образуют категорию [7] На наш взгляд это можно отнести к любой формализуемой теории.
… В то время как Теория множеств имеет дело с объектами, называемыми классами,для которых определено бинарное отношение принадлежности 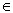 ( A
( A 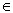 Bчитается: Aесть элемент B)
Bчитается: Aесть элемент B) [8] Это, в определенной степени, отражает главное феноменологическое свойство теории множеств, естественно в сопровождении существенного аксиоматического обрамления с целью исключения возможных парадоксов.
…, то, в отличие от этого, категориясостоит из класса, элементы которого называются объектами, и класса, элементы которого называются морфизмами » [9] На наш взгляд именно этот дуализм является принципиальной феноменологической особенностью абстракций теории категорий.
.
В нашем рассмотрении оставим в стороне вопросы полноты определения понятия «система». Остановимся лишь на введенном понятии границы системы. Такая стратификация порождает два указанных традиционных системных подхода, отражающих внутренний (имманентный – Im )и внешний (трансцендентный – Tr )аспекты представления системы.
Внешнее, прагматическое восприятие системы трансцендентным наблюдателем обычно связывается с возможностями ее взаимовлияния с внешней средой. В информационных системах такое представление ассоциируется с проблемной областью функционирования системы. Обозначим такое представление системы S TT (чисто трансцендентный взгляд). В какой-то степени одной из интерпретаций такого представления системы является понятие «черного ящика», при котором внешнему наблюдателю доступны лишь входные и выходные величины, а внутреннее устройство и процессы, протекающие в системе, неизвестны.
Реальное воплощение системных возможностей осуществляется на основе представления и реализацией трансцендентным наблюдателем перечня конкретных процедур, обеспечивающих согласованность процессов, протекающих во внешней среде, непосредственно с элементами системы. Это, как бы взгляд из внешней среды сквозь границу системы с целью реализации необходимого взаимодействия. Обозначим такое представление системы S TI (взгляд трансцендентного наблюдателя сквозь границу системы). Такое представление можно соотнести с понятием архитектуры .
Читать дальше

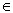 ( A
( A 




