Сергей Гаврилов - Полезные программы Python-3. Книга третья

# .... Конец листинга программы .....

Имеем три угла А, В и С

Листинг программы.

# -*– coding: cp1251 -*-

import math # Подключили математич модуль.

uu=" "

u=" Расчет элементов треугольника "

print (uu)

print (uu)

print (u)

print (uu)

u=" Напротив сторон треугольника лежат одноименные углы "

print (u)

print (uu)

u=" ...... ...... ...... ...... ...... ...... ..... ...... "

print (u)

print (uu)

Pii=0.000000

Pii=math.pi # Вытащили число " Пи "

print (uu)

print (uu)

print (uu)

u=" Известны три угла ( определяем пропорции сторон ) "

print (u)

print (uu)

u=" Введите угол А в градусах "

print (u)

print (uu)

au=0.00000000

au=input( ) # Вводим число

au=float(au) # Принудительно в вещественное число

u=" Введите угол B в градусах "

print (u)

print (uu)

bu=0.00000000

bu=input( ) # Вводим число

bu=float(bu) # Принудительно в вещественное число

cu=180-(au+bu)

cu=float(cu) # Принудительно в вещественное число

print (uu)

print (uu)

u=" .... ..... .... ..... "

print (u)

print (uu)

aur=au*Pii/180 # Угол C в радианах

bur=bu*Pii/180 # Угол C в радианах

cur=cu*Pii/180 # Угол C в радианах

a=1000*(math.sin(aur))

b=1000*(math.sin(bur))

c=1000*(math.sin(cur))

# " ,,,, ,,,, ,,,, ,,,,, ,,,,, ,,,, ,,,,, ,,,,, ,,,,, "

# Это « добавочный расчет »

# во все подпрограммы Треугольника

x=0.00000000

z=0.00000000

R=0.00000000

ha=0.00000000

hb=0.00000000

hc=0.00000000

z=math.sin(aur) # Sin угла A

R=a/(2*z) # R Описанной окружности

hc=b*z # Высота из угла С

z=math.sin(cur) # Sin угла С

hb=a*z # Высота из угла B

z=math.sin(bur) # Sin угла B

ha=c*z # Высота из угла A

S=a*ha/2 # Площадь треугольника

Pe=a+b+c # Периметр

rv=(S+S)/Pe # Радиус вписанной окружности

u=" ,,,, ,,,, ,,,, ,,,,, ,,,,, ,,,, ,,,,, ,,,,, ,,,,, "

print (uu)

print (u)

print (uu)

print (uu)

u=" Сторона A = "

ss=str(a) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Сторона B = "

ss=str(b) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Сторона C = "

ss=str(c) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Угол А = "

ss=str(au) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Угол B = "

ss=str(bu) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Угол C = "

ss=str(cu) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" .... ..... .... ..... ..... ..... .... ..... ..... "

print (u)

print (uu)

print (uu)

input( ) # Ожидание нажима Ентер

print (uu)

u=" Площадь = "

ss=str(S) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Радиус описанной окружности. = "

ss=str(R) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Радиус вписанной окружности = "

ss=str(rv) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Высота из угла A = "

ss=str(ha) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Высота из угла B = "

ss=str(hb) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Высота из угла C = "

ss=str(hc) # Преобразуем число в строку

u=u+ss

print (u)

print (uu)

u=" Центр тяжести на одной трети высоты "

print (u)

print (uu)

input( ) # Ожидание нажима Ентер

print (uu)

u=" ...... ...... ...... Конец программы ...... ...... ...... "

print (u)

print (uu)

input( ) # Ожидание нажима Ентер

print (uu)

# ..... ..... ..... Конец листинга программы ..... ....

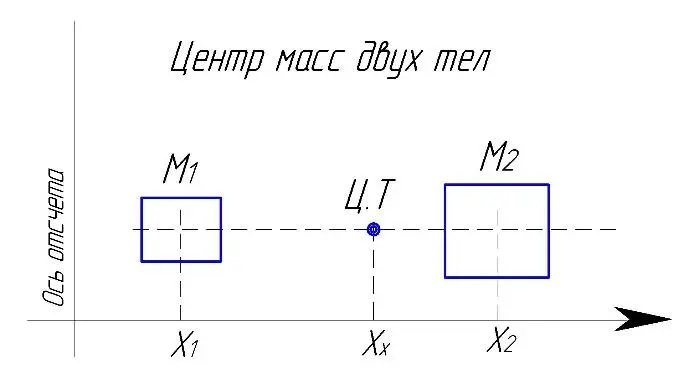
Определение координат центра масс нескольких тел производим методом последовательного добавления к уже определенной суммарной массе нескольких тел – еще одной массы. Начинаем с определения центра масс двух тел М1 и М2. Находим суммарную массу дух тел и координаты центра масс этих двух тел в точке Хх. Далее считаем, что сумма масс двух тел сосредоточена в точке центра масс с координатами Хх. Считаем что получившееся суммарное тело – это тело № М3. Затем добавляем к нему еще одно тело № М4. Снова получаем задачу по определению центра масс двух тел № М3 и № М4. Находим координаты новой точки центра масс. Программа позволяет добавлять к уже определенному суммарному телу еще одно тело столько раз – сколько необходимо.

По анологичной методике можно разработать программу по вычислению момента инерции, координат нейтральной оси и момента сопротивления тела сложной формы. Сечение тела сложной формы разбиваем на элементарные прямоугольники и расчитываем их как составное тело.

Листинг программы.

# -*– coding: cp1251 -*-

import sys # Подключили основные библиотеки

import math # Подключили математич модуль

uu=" "

print (uu)

print (uu)

print (uu)

u=" Расчет центра масс нескольких тел "

print (u)

u=" Введите массу первого тела М1 "

print (uu)

print (u)

m=0.0000

m=input( )

print (uu)

u=" Введите растояние до нулевой оси отсчета Х1 "

print (uu)