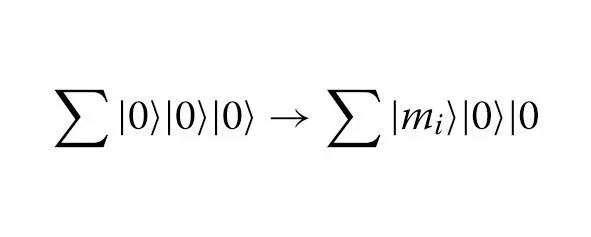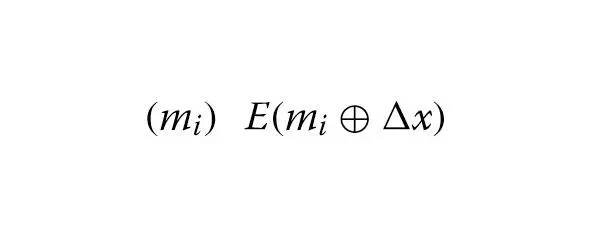Никита Шахулов - Атака на восстановление квантового ключа

Фактически, квантовый криптоанализ в модели Q2 существует уже давно. В 2010 году Кувакадо и Мори построили квантовый различитель на 3-круговой структуре Фейстеля (Kuwakado and Morii2010 г.) с использованием алгоритма Саймона в модели Q2. Затем они также восстановили ключ Even-Mansour, также используя алгоритм Саймона в 2012 году (Kuwakado and Morii2012 г.). На Crypto2016 Каплан и др. расширили результат в (Kuwakado and Morii2010 г.; 2012 г.) и применил алгоритм Саймона для атаки на ряд режимов шифрования и аутентифицированного шифрования, таких как CBC-MAC, PMAC, OCB (Kaplan et al. 2016a). В модели Q2 алгоритм Саймона может быть объединен с алгоритмом Гровера для применения в квантовом криптоанализе против блочных шифров. Леандер и Мэй (2017 г.) впервые использовал эту идею для атаки на FX-конструкцию в модели Q2. Вдохновленные этой работой, Донг и др. (2020a) дала атаку квантового восстановления ключа на полный цикл ГОСТ также в модели Q2. Кроме того, алгоритм Бернштейна-Вазарани (BV) (Bernstein and Vazirani1997 г.) также может быть применен в квантовом криптоанализе. Ли и Ян (2015 г.) предложил два метода выполнения квантового дифференциального криптоанализа на основе алгоритма BV. Затем Се и Ян расширили результат на Ли и Ян (2015 г.) и представить несколько новых методов атаки на блочные шифры с использованием алгоритма BV (Xie and Yang 2019 г.).

В модели Q1 кажется, что квантовый криптоанализ становится менее мощным. Самая тривиальная квантовая атака – это квантовый исчерпывающий поиск, который определяет общую безопасность блочных шифров в квантовой среде. Грассл и др. представляют квантовые схемы для реализации исчерпывающего поиска ключей на AES и оценки квантовых ресурсов в модели Q1 (Grassl et al.2016 г.). После этого есть также некоторые другие результаты, исследующие квантовую схему AES (Almazrooie et al.2018 г.; Jaques et al.2020 г.; Zou et al.2020 г.; Langenberg et al.2020 г.). Кроме того, существует множество попыток квантовых специализированных атак в сочетании с классическими методами криптоанализа, например дифференциальным и линейным криптоанализом (Kaplan et al.2016b), атаки встречей посередине (Хосоямада и Сасаки 2018 г.; Bonnetain et al.2019 г.) и рикошетные атаки (Хосоямада и Сасаки 2020 г.; Донг и др.2020b).

За последнее десятилетие исследованиям легковесных блочных шифров было уделено много внимания. Исследователи предложили несколько легких примитивов, чтобы назвать некоторые из них, SIMON (Beaulieu et al.2015 г.), SPECK (Beaulieu et al. 2015 г.), СКИННИ (Beierle et al. 2016 г.), НАСТОЯЩЕЕ (Богданов и др. 2007 г.). Чтобы подготовиться к будущему с крупномасштабными квантовыми компьютерами, необходимо изучить квантовую безопасность легких блочных шифров. Было предпринято несколько попыток изучить общие квантовые атаки на некоторые легкие блочные шифры (Anand et al.2020c; Jang et al.2020 г.; Ананд и др.2020b). В этой статье мы сосредоточимся на квантовой безопасности SIMON. Семейство алгоритмов SIMON (Beaulieu et al.2015 г.) – это легкий блочный шифр, предложенный NSA в 2013 году и обладающий выдающейся производительностью аппаратной реализации. В классической обстановке было много специализированных атак, направленных на SIMON. Однако в квантовой ситуации единственная квантовая атака на SIMON описана в Anand et al. (2020c), где Ананд и др. представить квантовую схему алгоритма Гровера на вариантах SIMON и дать соответствующую оценку квантовых ресурсов, которая является общей квантовой атакой. Для дальнейшего изучения квантовой безопасности SIMON нам необходимо изучить специальные квантовые атаки SIMON. Примечательно, что при измерении сложности атаки все существующие квантовые специализированные атаки изучали сложность шифрования, в то время как в нашем исследовании мы впервые использовали стоимость ресурсов квантовой схемы в качестве меры сложности.

Модель атакиМы рассматриваем атаку выбранного открытого текста на SIMON32 / 64 в модели Q1, где злоумышленник может делать классические онлайн-запросы оракула шифрования и может выбирать пары случайных сообщений с входным дифференциалом x. Чтобы осуществить такую атаку, противнику необходимо осуществить трансформацию:

qq

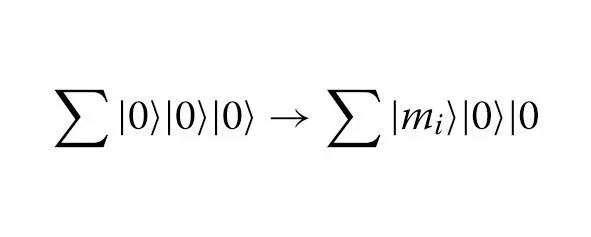
я знак равно1 я = 1

q

→ | mi | E |

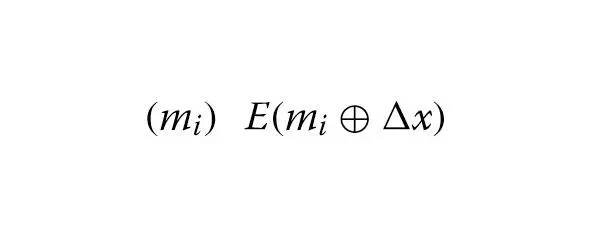
я = 1

когда задано q пар классической пары открытый текст-зашифрованный текст в качестве входных данных. Мы полагаем, что этот процесс эффективен. Таким образом, мы можем игнорировать стоимость квантовых ресурсов этого процесса.