Сергей Гаврилов - Расчеты в Excel

.xc=((f1*x1)+(f2*x2)+(f3*x3))/(f1+f2+f3)…

.r1=((h+hs+hm)-h/2)-xc… Радиус ц.т. головки от ц.т. рельса.

.r2=((hs/2)+hm)-xc… Радиус ц.т. стенки от ц.т. рельса.

.r3=xc-(hm/2)… Радиус ц.т. подошвы от ц.т. рельса.

.jx1=j1+(r1*r1*f1)… Момент инерции смещенной головки.

.jx2=j2+(r2*r2*f2)… Момент инерции смещенной стенки.

.jx3=j3+(r3*r3*f3)… Момент инерции смещенной подошвы.

.jx=jx1+jx2+jx3… Момент инерции рельса по ХХ.

.wx1=jx/((h+hs+hm)-xc)… Момент сопротивления изгибу рельса по ХХ.

.wx=jx/xc… Момент сопротивления изгибу рельса по ХХ.

Берем меньшее значение W из двух значений…

.jy1=h*b*b*b/12…

.jy2=hm*bm*bm*bm/12…

.jy3=hs*bs*bs*bs/12…

.jy=jy1+jy2+jy3… Момент инерции рельса по Y.

Выбор максимально удаленной части для оси Y-Y.

.wy=jy/(b/2)… Момент сопротивления изгибу рельса по YY.

.wy=jy/(bm/2)… Момент сопротивления изгибу рельса по YY.

Берем меньшее значение W из двух значений…

Выбираем меньшее значение момента инерции «j».

.rm=sqrt(jx/s)…

.rm=sqrt(jy/s)…

Запись программы в Excel.

Смотри открытый и закрытый листы Е 24.. ( Скачать из приложения ).

В колонке «Е»расчет промежуточных величин.

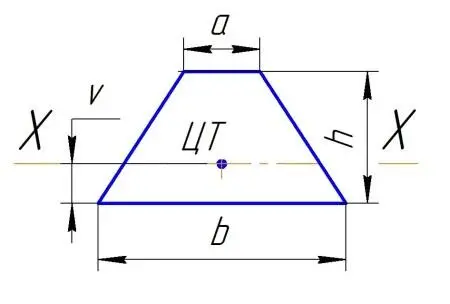
Параметры сечения трапеции

Высота трапеции = h.

Верх трапеции = a.

Основание трапеции = b.

Ось Х-Х проходит через Ц.Т. и параллельна основанию.

Ось Y-Y проходит через Ц.Т. и перпендикулярна основанию.

Рис. Сечение трапеции.

# Ведем расчет по классическим формулам 14-03-2020 г..

Pii = 3,141592654… Число Пи.

.x=(b-a)/2..

.y=(h*h)+(x*x)..

.ab=sqrt(y).. # Извлекаем квадратный корень ( Боковая грань трапеции ).

.xx=((a+x)*(a+x))+(h*h)..

.dt=sqrt(xx).. # Извлекаем квадратный корень (Диагональ трапеции ).

Ugrx=h/x..

Ugr=arctan(Ugrx).. # АрксТангенс от Ugrx в радианах.

Ug=Ugr*180/Pii.. # Угол в градусах…( Угол при основании ).

.s=h*(b+a)/2.. Площадь трапеции.

Далее расчет по оси Х-Х ( Ось Х-Х параллельна основанию ).

Разложим трапецию на два треугольника и на прямоугольник.

Sp=a*h.. # Площадь прямоугольника.

Jp=h*h*h*a/12.. # Момент инерции прямоугольника.

St=((b-a)/2)*h/2.. # Площадь одного треугольника.

.x=(b-a)/2.. # Основание одного треугольника.

Jt=h*h*h*x/36.. # Момент инерции одного треугольника.

.yt=h/3.. # Нейтральная ось от основания треугольника.

# Центр тяжести системы от основания ( нейтральная ось ).

.z=(((St+St)*yt)+(Sp*h/2))/(St+St+Sp).. ( На рисунке z обозначена как V ).

# Момент инерции двух треугольников со смещенным центром.

.at=z-yt.. # Смещение центра тяжести треугольников относительно Ц.Т. трапеции.

Момент инерции двух треугольников по Х-Х со смещенным центром.

Jts=2*(Jt+at*at*(St))..

# Момент инерции прямоугольника по Х-Х со смещенным центром.

.ap=z-(h/2).. # Смещение центра прямоугольника относительно Ц.Т. трапеции.

Jps=Jp+ap*ap*Sp.. Момент инерции прямоугольника по Х-Х со смещенным центром.

.jx=Jps+Jts.. # Момент инерции трапеции по оси ХХ.

.v=z.. # От основания – до нейтральной оси трапеции.

.wxv=jx/(h-v).. # Момент сопротивления изгибу для верхнего основания X-X.

.wxn=jx/v.. # Момент сопротивления изгибу для нижнего основания X-X.

.xr=jx/(Sp+St+St).. # jx / Площадь трапеции.

Rix=sqrt(xr).. # Извлекаем квадратный корень ( Радиус инерции ).

Далее расчет по оси YY.

# Разложим трапецию на два треугольника и на прямоугольник.

Sp=a*h.. # Площадь прямоугольника.

Jpy=a*a*a*h/12.. # Момент инерции прямоугольника.

# …

St=((b-a)/2)*h/2.. # Площадь одного треугольника.

.hy=(b-a)/2.. # Высота одного треугольника.

Jty=hy*hy*hy*h/36.. # Момент инерции одного треугольника Y-Y.

.yty=hy/3.. # Нейтральная ось от основания треугольника.

.ytyc=yty+(a/2).. # Нейтральная ось треугольника от оси Y-Y.

# Момент инерции двух треугольников со смещенным центром.

# .ytyc – Смещение центра треугольников от оси Y-Y.

Jtsy – Момент инерции двух треугольников по Y-Y со смещенным центром.

Jtsy=2*(Jty+ytyc*ytyc*(St))..

# Jpy – Момент инерции прямоугольника ( смещения нет ).

.jyy=Jpy+Jtsy.. # Момент инерции трапеции по оси Y-Y.

.wyv=jyy/(b/2).. # Момент сопротивления изгибу для Y-Y.

.xr=jyy/(Sp+St+St).. # ( jx / Площадь трапеции ).

Riy=sqrt(xr).. # Извлекаем квадратный корень ( Радиус инерции по Y-Y ).

Контрольный расчет:

Сечение в виде симметричной трапеции.

Высота трапеции = 30.

Основание трапеции = 50.

Верх трапеции = 20.

…

Боковая грань трапеции = 33.54102.

Диагональ трапеции = 46.097722.

Угол при основании = 63.434949 Градус.

Площадь трапеции = 1050.0.

Далее расчет по оси Х-Х.

Момент инерции по Х-Х одного треугольника Jt = 11250.0.

Центр тяжести системы Х-Х от основания = 12.8571.

Момент инерции двух треугольников по Х-Х со смещенным центром. = 26173.4694.