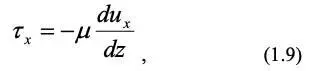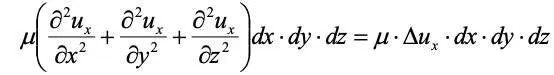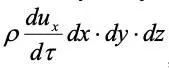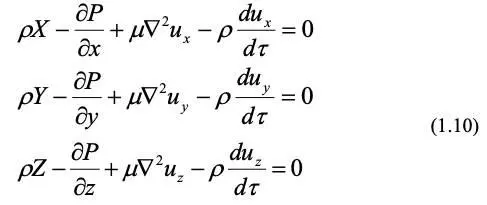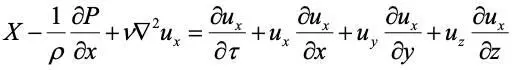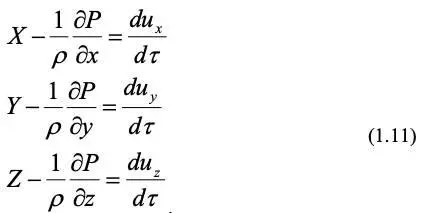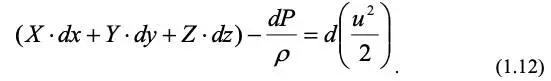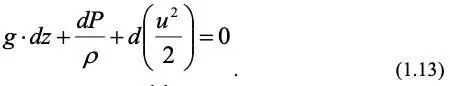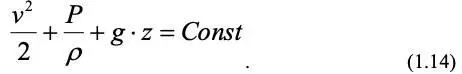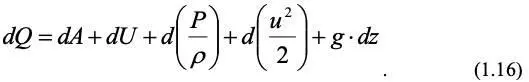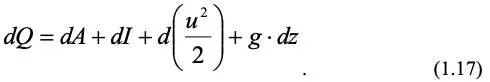На верхнюю и нижнюю грани действуют силы вязкостного трения. Их проекция на ось х составит 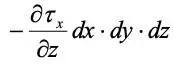 .
.
С учетом закона Ньютона для вязкостного трения:
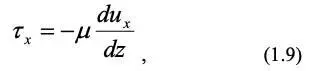
имеем проекцию сил вязкостного трения на ось х :
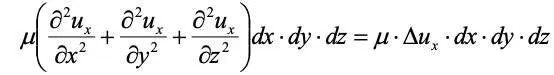
.
Здесь выражение в скобках – оператор Лапласа от проекции скорости на ось х, он обозначается Δ u xили 2 u x.
Так как сумма проекций всех сил равна проекции силы инерции:
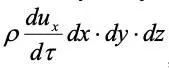
,
относя все силы к единице объема, получим:
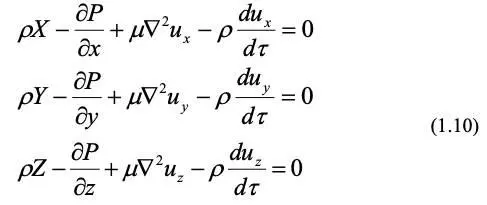
Последние два уравнения получены аналогично для осей у и z, а в целом система уравнений (1.10) в гидрогазодинамике называется уравнениями движения вязкой жидкости Навье-Стокса и выражает закон сохранения количества движения.
Система уравнений Навье-Стокса может быть записана более детально, если раскрыть полную производную проекции скорости. Так уравнение для оси х, например, при делении всех его членов на ρ , c учетом, что ν = μ/ρ, будет иметь вид:
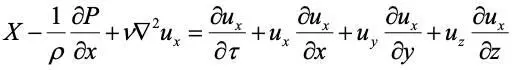
.
Аналогично записываются уравнения для осей у и z.
1.3 Закон сохранения энергии
Рассмотрим сначала закон сохранения энергии для движения идеальной жидкости. Так как в идеальной жидкости отсутствуют силы вязкостного трения, то для этого случая из системы уравнений (1.10), положив проекции силы вязкости равным нулю, получим следующую систему (система уравнений движения идеальной жидкости Эйлера):
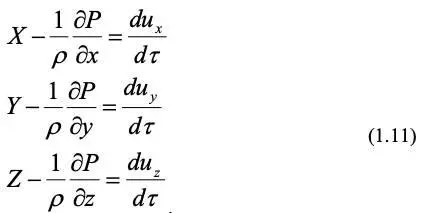
.
Помножим эти уравнения соответственно на dx , dy , dz и сложим. Тогда, преобразуя, получим следующее уравнение:
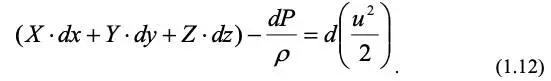
В поле силы тяжести ( Х = 0; У = 0; Z = – g ) уравнение (1.12) примет вид:
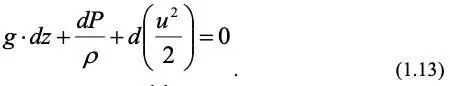
Это уравнение определяет в дифференциальном виде закон сохранения энергии для движения идеальной жидкости и представляет собой, соответственно, сумму удельных (отнесенных к единице массы) потенциальных энергий положения и давления и кинетической энергии. При интегрировании уравнения (1.13) для потока несжимаемой жидкости (ρ = Const) получим уравнение Бернулли для одномерного потока, движущегося со средней скоростью v:
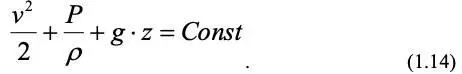
Уравнение Бернулли показывает, что для идеальной жидкости сумма потенциальной и кинетической энергий остается постоянной вдоль всего потока.
В более общей форме закон сохранения энергии описывает 1-й закон термодинамики: теплота, подводимая к системе, идет на производство работы и увеличение энергии системы:

Выражение для потока энергии в дифференциальном виде включает ее члены, входящие в уравнение (1.13) плюс, внутренняя энергия dU . С учетом этого запишем уравнение (1.15) в следующем виде:
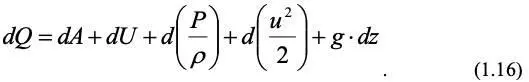
Сумма второго и третьего членов правой части уравнения (1.16) представляет собой изменение энтальпии dh . С учетом этого получим другой вид уравнения (1.16):
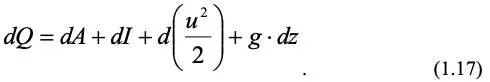
1.4 Микро- и макроперенос
Молекулярный перенос, называемый еще микропереносом, происходит вследствие беспорядочного теплового движения микрочастиц (броуновское движение), когда среда в целом неподвижна. Перенос массы при наличии молекулярного переноса называется молекулярной диффузией. Перенос тепла под действием молекулярного переноса называется теплопроводностью. Перенос количества движения под действием молекулярного переноса происходит при наличии молекулярного (вязкостного) трения при ламинарном движении среды. Процесс микропереноса описывается микрокинетикой.
Читать дальше

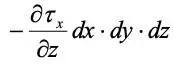 .
.