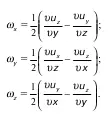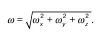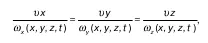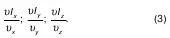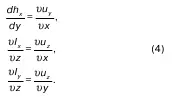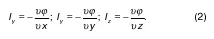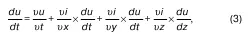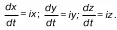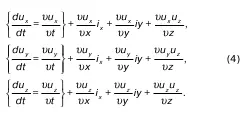М. Бабаев - Гидравлика

Особенности видов движения, рассматриваемых в гидродинамике.

Можно выделить следующие виды движения.

Неустановившееся, по поведению скорости, давления, температуры и т. д.; установившееся, по тем же параметрам; неравномерное, в зависимости от поведения тех же параметров в живом сечении с площадью; равномерное, по тем же признакам; напорное, когда движение происходит под давлением p > p атм, (например, в трубопроводах); безнапорное, когда движение жидкости происходит только под действием силы тяжести.

Однако основными видами движения, несмотря на большое количество их разновидностей, являются вихревое и ламинарное движения.

Движение, при котором частицы жидкости вращаются вокруг мгновенных осей, проходящих через их полюсы, называют вихревым движением.

Это движение жидкой частицы характеризуется угловой скоростью, компонентами (составляющими), которой являются:

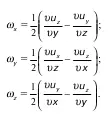
Вектор самой угловой скорости всегда перпендикулярен плоскости, в которой происходит вращение.

Если определить модуль угловой скорости, то

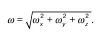
Удвоив проекции на соответствующие координаты оси ω x, ω y, ω z, получим компоненты вектора вихря

θ = 2ω.

Совокупность векторов вихря называется векторным полем.

По аналогии с полем скоростей и линией тока, существует и вихревая линия, которая характеризует векторное поле.

Это такая линия, у которой для каждой точки вектор угловой скорости сонаправлен с касательной к этой линии.

Линия описывается следующим дифференциальным уравнением:

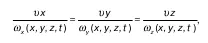
в котором время t рассматривается как параметр.

Вихревые линии во многом ведут себя так же, как и линии тока.

Вихревое движение называют также турбулентным.

Это движение, называют также потенциальным (безвихревым) движением.

При таком движении отсутствует вращение частиц вокруг мгновенных осей, которые проходят через полюсы жидких частиц. По этой причине:

υ x= 0; υ y= 0; υ z= 0. (1)

ω x= ω y= ω z= 0.

Выше отмечалось, что при движении жидкости происходит не только изменение положения частиц в пространстве, но и их деформация по линейным параметрам. Если рассмотренное выше вихревое движение является следствием изменения пространственного положения жидкой частицы, то ламинарное (потенциальное, или безвихревое) движение является следствием деформационных явлений линейных параметров, например, формы и объема.

Вихревое движение определялось направлением вихревого вектора

где υ – угловая скорость, которая является характеристикой угловых деформаций.

Деформацию этого движения характеризируют деформацией этих компонентов

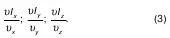
Но, поскольку при ламинарном движении υ x=υ y= υ z= 0, то:

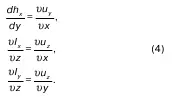
Из этой формулы видно: поскольку существуют частные производные, связанные между собой в формуле (4), то эти частные производные принадлежат некоторой функции.

φ = φ(x, y, z) (1)

Функция φ называется потенциалом скорости.

С учетом этого, компоненты φ выглядят следующим образом:

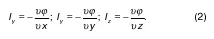
Формулой (1) описывается неустановившееся движение, поскольку она содержит параметр t.

Ускорение при ламинарном движении

Ускорение движения жидкой частицы имеет вид:

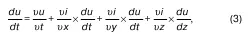
где du/dt – полные производные по времени.

Ускорение можно представить в таком виде, исходя из

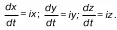
Составляющие искомого ускорения

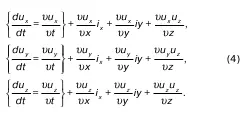
Формула (4) содержит в себе информацию о полном ускорении.