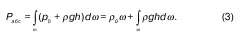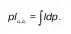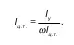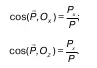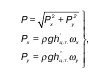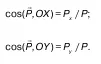М. Бабаев - Гидравлика

При наклонности плоскости дна имеет место смачивание поверхности с площадью ω. Поэтому, в отличие от предыдущего случая, когда дно лежало в горизонтальной плоскости, нельзя сказать, что давление постоянно.

Чтобы определить его, разобьем площадь ω на элементарные площади dω, на любую из которых действует давление

По определению силы давления,

причем dP направлено по нормали к площадке ω.

Теперь, если определить суммарную силу которая воздействует на площадь ω, то ее величина:

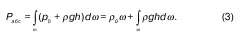
Определив второе слагаемое в (3) найдем Р абс.

Pабс = ω(p 0+ h ц. е). (4)

Получили искомые выражения для определения давлений, действующих на горизонтальную и наклонную

плоскости: Р изби Р абс.

Рассмотрим еще одну точку С, которая принадлежит площади ω, точнее, точку центра тяжести смоченной площади ω. В этой точке действует сила P 0= ρ 0ω.

Сила действует в любой другой точке, которая не совпадает с точкой С.

При расчетах в гидротехнике интерес представляет сила избыточного давления Р, при:

р 0= р атм,

где р0 – давление, приложенное к центру тяжести.

Говоря о силе, будем иметь в виду силу, приложенную в центре давления, хотя будем подразумевать, что это – сила избыточного давления.

Для определения Р абс воспользуемся теоремой моментов, из теоретической механики: момент равнодействующей относительно произвольной оси равен сумме моментов составляющих сил относительно той же оси.

Теперь, согласно этой теореме о равнодействующем моменте:

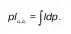
Поскольку при р 0= р атм, P = ρgh ц. е.ω, поэтому dP = ρghd ω= ρgsinθld ω, следовательно (здесь и далее для удобства не будем различать р изби р абс), с учетом P и dP из (2), а также после преобразований следует:

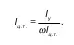
Если теперь перенесем ось момента инерции, то есть линию уреза жидкости (ось O Y) в центр тяжести ω, то есть в точку С, то относительно этой оси момент инерции центра давления точки D будет J 0.

Поэтому выражение для центра давления (точка D) без переноса оси момента инерции от той же линии уреза, совпадающие с осью O Y, будет иметь вид:

I y= I 0+ ωl 2 ц.т.

Окончательная формула для определения места расположения центра давления от оси уреза жидкости:

l ц. д.= l ц. г.+ I 0/S.

где S = ωl ц.д.– статистический момент.

Окончательная формула для l ц.д.позволяет определить центр давления при расчетах гидротехнических сооружений: для этого разбивают участок на составные участки, находят для каждого участка l ц.д.относительно линии пересечения этого участка (можно пользоваться продолжением этой линии) со свободной поверхностью.

Центры давления каждого из участков находятся ниже центра тяжести смоченной площади по наклонной стенке, точнее по оси симметрии, на расстоянии I 0/ωl ц.u.

1. В общем случае, это давление:

P z= ρgWg,

где Wg – обьем рассматриваемой призмы.

В частном случае, направления линий действия силы на криволинейную поверхность тела, давления зависят от направляющих косинусов следующего вида:

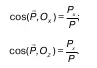
Сила давления на цилиндрическую поверхность с горизонтальной образующей полностью определена. В рассматриваемом случае ось O Yнаправлена параллельно горизонтальной образующей.

2. Теперь рассмотрим цилиндрическую поверхность с вертикальной образующей и направим ось O Zпараллельно этой образующей, что значит ω z= 0.

Поэтому по аналогии, как и в предыдущем случае,

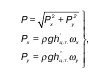
где h' ц.т.– глубина центра тяжести проекции под пьезометрическую плоскость;

h' ц.т.– то же самое, только для ω y.

Аналогично, направление определяется направляющими косинусами

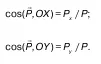
Если рассмотреть цилиндрическую поверхность, точнее, объемный сектор, с радиусом γ и высотой h, с вертикальной образующей, то

ω x= h y,

h' ц.т.= 0,5h.

3. Осталось обобщить полученные формулы для прикладного применения произвольной криволинейной поверхности: