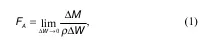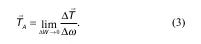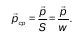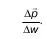М. Бабаев - Гидравлика

2. Сжимаемость.

3. Плотность.

4. Объемное сжатие.

5. Вязкость.

6. Температурное расширение.

7. Сопротивление растяжению.

8. Свойство растворять газы.

9. Поверхностное натяжение.

Жидкости делятся на покоящиесяи движущиеся.

Здесь же рассмотрим силы, которые действуют на жидкость и вне ее в общем случае.

Сами эти силы можно разделить на две группы.

1. Силы массовые.По-другому эти силы называют силами, распределенными по массе: на каждую частицу с массой Δ M = ρ W действует сила Δ F , в зависимости от ее массы.

Пусть объем Δ W содержит в себе точку А . Тогда в точке А :

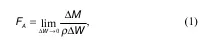
где FА – плотность силы в элементарном объеме.

Плотность массовой силы – векторная величина, отнесена к единичному объему Δ W ; ее можно проецировать по осям координат и получить: Fx, Fy, Fz . То есть плотность массовой силы ведет себя, как массовая сила.

Примерами этих сил можно назвать силы тяжести, инерции (кориолисова и переносная силы инерции), электромагнитные силы.

Однако в гидравлике, кроме особых случаев, электромагнитные силы не рассматривают.

2. Поверхностные силы.Таковыми называют силы, которые действуют на элементарную поверхность Δ w , которая может находиться как на поверхности, так и внутри жидкости; на поверхности, произвольно проведенной внутри жидкости.

Таковыми считают силы: силы давления которые составляют нормаль к поверхности; силы трения которые являются касательными к поверхности.

Если по аналогии (1) определить плотность этих сил, то:

нормальное напряжение в точке А :

касательное напряжение в точке А :

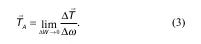
И массовые, и поверхностные силы могут быть внешними, которые действуют извне и приложены к какой-то частице или каждому элементу жидкости; внутренними, которые являются парными и их сумма равна нулю.

Общие дифференциальные уравнения равновесия жидкости – уравнения Л. Эйлера для гидростатики.

Если взять цилиндр с жидкостью (покоящейся) и провести через него линию раздела, то получим жидкость в цилиндре из двух частей. Если теперь приложить некоторое усилие к одной части, то оно будет передаваться другой через разделяющую плоскость сечения цилиндра: обозначим эту плоскость S = w .

Если саму силу обозначить как то взаимодействие, передаваемое от одной части к другой через сечение Δ w , и есть гидростатическое давление.

Если оценить среднее значение этой силы,

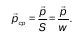
Рассмотрев точку А как предельный случай w , определяем:

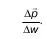
Если перейти к пределу, то Δ w переходит в точку А .

Поэтому Δp x→ Δp n. В конечном результате px = pn , точно так же можно получить p y = p n, p z = p n .

Следовательно,

p y = p n, p z = p n .

Мы доказали, что во всех трех направлениях (их мы выбрали произвольно) скалярное значение сил одно и то же, то есть не зависит от ориентации сечения Δ w .

Вот это скалярное значение приложенных сил и есть гидростатическое давление, о котором говорили выше: именно это значение, сумма всех составляющих, передается через Δ w .

Другое дело, что в сумме ( p x + p y + p z ) какая-то составляющая окажется равной нулю.

Как мы в дальнейшем убедимся, в определенных условиях гидростатическое давление все же может быть неодинаково в различных точках одной и той же покоящейся жидкости, т. е.

p = f ( x, y, z ).

Свойства гидростатического давления.

1. Гидростатическое давление всегда направлено по нормали к поверхности и его величина не зависит от ориентации поверхности.

2. Внутри покоящейся жидкости в любой точке гидростатическое давление направлено по внутренней нормали к площадке, проходящей через эту точку.

Причем p x = p y = p z = p n .

3. Для любых двух точек одного и того же объема однородной несжимаемой жидкости (ρ = const)