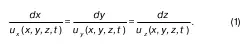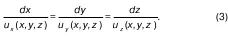М. Бабаев - Гидравлика

Гидростатика изучает жидкость в ее равновесном состоянии.

Кинематика жидкости изучает жидкость в движении, не рассматривая сил, порождавших или сопровождавших это движение.

Гидродинамика также изучает движение жидкости, но в зависимости от воздействия приложенных к жидкости сил.

В кинематике используется сплошная модель жидкости: некоторый ее континуум. Согласно гипотезе сплошности, рассматриваемый континуум – это жидкая частица, в которой беспрерывно движется огромное количество молекул; в ней нет ни разрывов, ни пустот.

Если в предыдущих вопросах, изучая гидростатику, за модель для изучения жидкости в равновесии взяли сплошную среду, то здесь на примере той же модели будут изучать жидкость в движении, изучая движение ее частиц.

Для описания движения частицы, а через нее и жидкости, существуют два способа.

1. Метод Лагранжа. Этот метод не используется при описании волновых функций. Суть метода в следующем: требуется описать движение каждой частицы.

Начальному моменту времени t 0соответствуют начальные координаты x 0, y 0, z 0.

Однако к моменту t они уже другие. Как видно, речь идет о движении каждой частицы. Это движение можно считать определенным, если возможно указать для каждой частицы координаты x, y, z в произвольной момент времени t как непрерывные функции от x 0, y 0, z 0.

x = x(x 0, y 0, z 0, t)

y =y (x 0, y 0, z 0, t)

z = z(x 0, y 0, z 0, t) (1)

Переменные x 0, y 0, z 0, t, называют переменными Лагранжа.

2. Метод определения движения частиц по Эйлеру. Движение жидкости в этом случае происходит в некоторой неподвижной области потока жидкости, в котором находятся частицы. В частицах произвольно выбираются точки. Момент времени t как параметр является заданным в каждом времени рассматриваемой области, которая имеет координаты x, y, z.

Рассматриваемая область, как уже известно, находится в пределах потока и неподвижна. Скорость частицы жидкости u в этой области в каждый момент времени t называется мгновенной местной скоростью.

Полем скорости называется совокупность всех мгновенных скоростей. Изменение этого поля описывается следующей системой:

u x= u x(x,y,z,t)

u y= u y(x,y,z,t)

u z= u z(x,y,z,t)

Переменные в (2) x, y, z, t называют переменными Эйлера.

Сутью вышеупомянутого поля скоростей являются векторные линии, которые часто называют линиями тока.

Линия тока – такая кривая линия, для любой точки которой в выбранный момент времени вектор местной скорости направлен по касательной (о нормальной составляющей скорости речь не идет, поскольку она равна нулю).

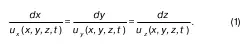
Формула (1) является дифференциальным уравнением линии тока в момент времени t. Следовательно, задав различные ti по полученным i, где i = 1,2, 3, …, можно построить линию тока: ею будет огибающая ломаной линии, состоящей из i.

Линии тока, как правило, не пересекаются в силу условия ≠ 0 или ≠ ∞. Но все же, если эти условия нарушаются, то линии тока пересекаются: точку пересечения называют особой (или критической).

1. Неустановившееся движение, которое так называется иззза того, что местные скорости в рассматриваемых точках выбранной области по времени изменяются. Такое движение полностью описывается системой уравнений.

2. Установившееся движение: поскольку при таком движении местные скорости не зависят от времени и постоянны:

u x= u x(x,y,z)

u y= u y(x,y,z)

u z= u z(x,y,z)

Линии тока и траектории частиц совпадают, а дифференциальное уравнение для линии тока имеет вид:

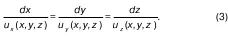
Совокупность всех линий тока, которые проходят через каждую точку контура потока, образует поверхность, которую называют трубкой тока. Внутри этой трубки движется заключенная в ней жидкость, которую называют струйкой.

Струйка считается элементарной, если рассматриваемый контур бесконечно мал, и конечной, если контур имеет конечную площадку.

Сечение струйки, которое нормально в каждой своей точке к линиям тока, называется живым сечением струйки. В зависимости от конечности или бесконечной малости, площадь струйки принято обозначать, соответственно, ω и dω.

Некоторый объем жидкости, который проходит через живое сечение в единицу времени, называют расходом струйки Q.