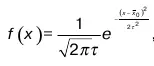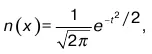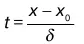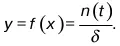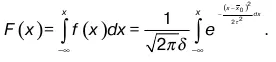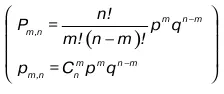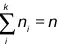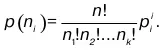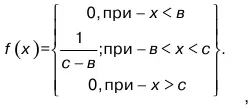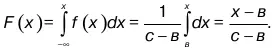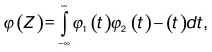Закон нормального распределения (закон Гаусса). Практика неуклонно подтверждает, что закону Гаусса с достаточным приближением подчиняются законы распределения ошибок при измерениях самых различных параметров: от линейных и угловых размеров до характеристик основных механических свойств стали.
Плотность вероятности закона нормального распределения (в дальнейшем Н. Р.) имеет вид
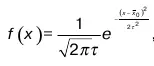
где x 0– среднее значение случайной величины;
τ – среднее квадратическое отклонение той же случайной величины;
e = 2,1783… – основание натурального логарифма;
Ж – параметр, который удовлетворяет условию.
Причина широкого применения закона нормального распределения теоретически определяется теоремой Ляпунова.
При известных Х 0и δ ординаты кривой функции f(x) можно вычислить по формуле
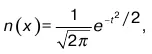
где t – нормированная переменная,
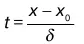
(t) плотность вероятности z. Если подставить z и (t) в формулу, то следует:
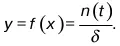
Кривую З.Н.Р. часто называют кривой Гаусса, этот закон описывает очень многие явления в природе.
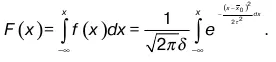
10. Биноминальный и полиноминальный законы распределения. Равновероятное распределение. Закон распределения эксцентриситета
1. Биноминальный закон распределения. Этот закон математически выражается формулой разложения бинома (q + p) 2 в следующем виде
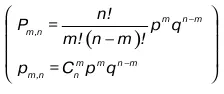
где n! – читается как n-факториал,
C n m– биноминальный коэффициент, выражающий количество сочетаний из n элементов по m, причем, n – положительное целое число.
2. Полиномиальный закон распределения (П/З/Р).В предыдущем случае рассмотрено два исхода появления случайного события А: или оно появится с вероятностью р, или не появится с вероятностью q = 1 – p.
Когда количество независимых испытаний равно n, то велика вероятность того, что каждое событие V iпроизойдет n раз, где i =1, 2,..., k. Причем
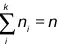
определяется формулой
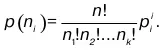
В виде формулы (58) получен искомый полиномиальный полиноминальный закон распределения.
3. Равновероятное распределение.Рассматривая вышеприведенные законы распределения случайной величины, пришлось подчеркнуть различия в их проявлении при условиях: прерывно ли распределение случайных величин или непрерывно?
Другое название этого закона – равномерное, или прямоугольное распределение, несет в себе больше информации о кривой этого закона. Вероятность наступления случайного события А на рассматриваемом промежутке одинакова в любой точке из промежутка[в; с]. Для Р/Р плотность
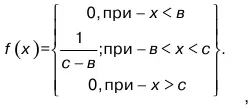
где в, с – параметры З/Р/Р.
Функция распределения для З/Р/Р имеет вид:
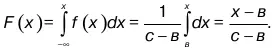
11. Другие законы распределения
В технической промышленности, в том числе приборостроении, применяются некоторые другие виды законов распределения, кроме вышерассмотренных. При этом распределение случайных величин идет уже по самым разнообразным их параметрам. Приведем краткое изложение еще трех законов распределения случайной величины.
1. Композиция законов распределения, так называют закон распределения суммы случайных величин, причем слагаемые суммы заданы предварительно.
Если рассмотреть случайную переменную Ж = X + Y, где X и Y имеют соответствующие плотности вероятности и независимы, то плотность вероятности Z
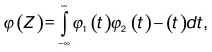
где t выступает как переменная интеграции. Замечено: какому закону распределения следуют X и Y, тому же следует Z.
Читать дальше
Конец ознакомительного отрывка
Купить книгу