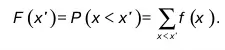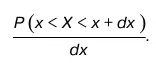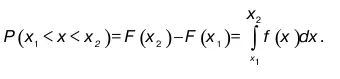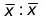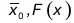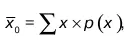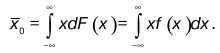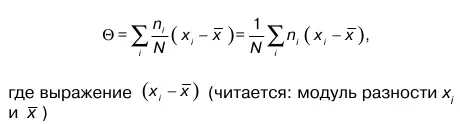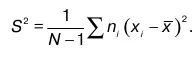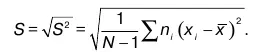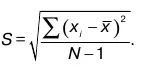Зависимость между возможными значениями случайных величин и их вероятностями, выраженными конкретным способом, называется законом распределения случайных величин.
Для того, чтобы установить математическую форму этого закона, предположим, что дискретная случайная величина х может принимать значения х 1 , x 2 , x 3 …, х i…., x k , и пусть каждому из этих значений соответствует вероятность P x. Тогда ряд вероятностей, соответствующих значениям случайной величины х, будет иметь следующий вид P x,P x1,P x2,…,P xi,…,P xk.
Очевидно, что вероятность P xявляется некоторой функцией от переменной х и имеет вид: P x= f(х), где x = x i, i = 1, 2…, k.
Рассмотрим поведение этой функции для вышеприведенных двух видов случайных величин.
1. Случайная величина – дискретная (прерывная).
Случайная величина х < х', где х < х' задано, может выражаться следующим образом:
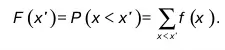
Функция F(х)=F(х') называется функцией распределения случайной прерывной величины ч. 2. Случайная величина – непрерывна. Плотностью вероятности P xв точке X = х называется предел вида
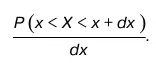
Следовательно, функцию F(х') можно дифференцировать, тогда
F ( х )= f ( х )
Основные свойства функции распределения следующие:
1) х = ∞;F(∞)= 1;
2) х = —∞;F(∞) = 0;
3) если аргумент x возрастает, т. е. если рассмотреть случай х 2 > х 1 , то F(x 2 ) > F(x 1 ).
Если рассмотреть ΔF(х)=F(х 2 )-F (х 1 ) то
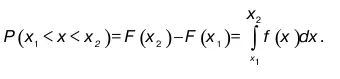
6. Статистика распределения случайных величин
Основные характеристики случайных величин.
1. Меры положения.
Таковыми называют (считают) точки, вокруг которых происходит колебание характеристики величин.
Сумма произведений эмпирических значений случайной величены x iна соответствующие частности называется выборочным средним
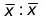
– это статистическая характеристика, соответствующая параметрам, т. е. теоретическому анализу, называемая средним значением случайной величины или математическим ожиданием случайной величины.
Математическое ожидание обозначается как
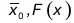
или м.о.(х), и определяется по уже известному теоретическому распределению.
При прерывности случайной величины
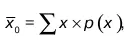
где p(x) – функция, которая определяет вероятности p(x) для всех x iслучайной величины. При непрерывности случайной величины
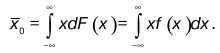
где f(x) – плотность вероятности,
F(x) – функция распределения случайной величины.
Кроме вышеприведенных оперируют следующими мерами положения:
1) среднее гармоническое;
2) среднее логарифмическое;
3) скользящее среднее;
4) накопленное среднее.
Но эти меры используются не очень часто.
2. Меры рассеяния.
Если меры положения характеризовали точки, вокруг которых происходило колебание значений случайных величин, то меры рассеяния характеризуют группировку самих значений колеблющейся величины x или x i
Подхарактеристика мер рассеяния:
1. Выборочное среднее абсолютное отклонение
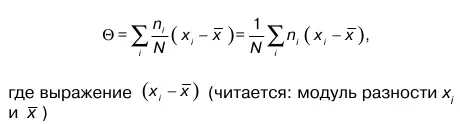
– абсолютное отклонение наблюденного значения xi случайной величины от выборочного среднего.
2. Выборочная дисперсия S 2 ; она характеризует рассеяние или однородность случайной величины x i
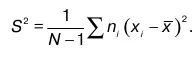
7. Выборочное среднеквадратичное отклонение
Эта характеристика пользуется наибольшей популярностью:
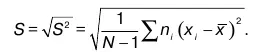
При n 1= n 2=... = n k= 1, т. е. в случае несведения в разряды наблюденных значений x i,
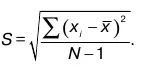
Дисперсией δ 2теоретического распределения прерывной случайной переменной является математическое ожидание квадрата отклонения случайной величины х от ее определенного значения x о ,т. е.
Читать дальше
Конец ознакомительного отрывка
Купить книгу