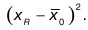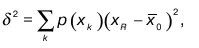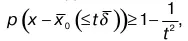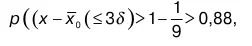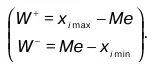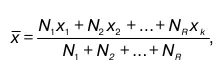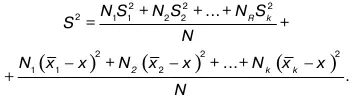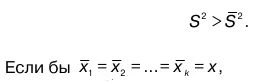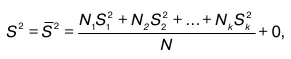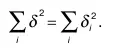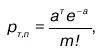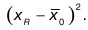
Это математическое ожидание представляет собой: если случайная величина прерывная, то
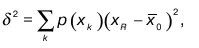
где p(x k) – вероятность случайной величины х k
Роль в теории вероятности среднего квадратичного отклонения наглядно показывает неравенство Чебы-шева, которое имеет вид:
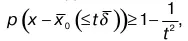
где x – случайная величина;
х о– ее математическое ожидание;.
f > 0 – некоторый численный коэффициент.
Если взять t = 3, то из (40) следует:
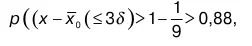
что означает вероятность отклонения случайной величины x от своего среднего значения на величину большую, чем 3δ. Причем полученный результат справедлив при любом теоретическом распределении.
Как разновидностью меры рассеяния в приборостроении, пользуются коэффициентом изменчивости – вариации.
3. Еще одной важной разновидностью меры рассеяния в приборостроении для статистического анализа и контроля является размах выборки W, его также называют широтой эмпирического распределения.
W = x imax= x imin
Как видно из формулы, размах выборки характеризует однородность наблюденных значений случайной величины х г В зависимости от знака W, можно заключить об отношении случайной величины к мере положения (конкретно, выборочной медиане), что и видно из следующей системы:
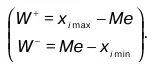
8. Теоремы о средних значениях и дисперсиях
Теоремы о средних значениях и дисперсиях дают представление о том, как себя поведут средние значения и дисперсии при объединении нескольких выборок, у каждой из которых есть свое средневзвешенное значение случайной величины.
Пусть объемы N 1, N 2, ... ,N k, которые имеют соответствующие средневзвешенные х 1 , x 2 , …, x k , объединены в одно.
Теорема 1. Математическое ожидание (среднее значение) суммы случайных величин равно сумме их математических ожиданий (средних значений).
То есть математическое ожидание суммы
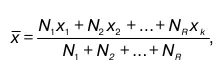
точно так же себя ведет дисперсия.
Теорема 2. Дисперсия объединенной выборки S 2 равна средневзвешенной из дисперсий отдельной выборки, сложенной с дисперсией средних xi частных выборок, т. е. если дисперсии S 1 2,S 2 2, …,S k 2־ принадлежат выборкам N 1, N 2, ... ,N k, то в случае объединения этих выборок общая дисперсия
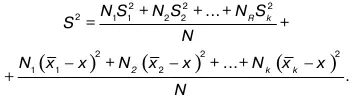
Очевидно, что объемы N1, N2, Nkобъединены в одну выборку с соответствующими дисперсиями
S 1 2,S 2 2, …,S k 2
Вторым слагаемым является дисперсия средних x iчастных выборок около среднего объединенной выборки х. Поэтому очевидно, что
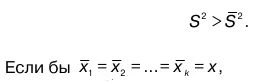
то второе слагаемое тоже равнялось бы нулю. В таком случае
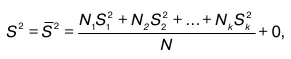
где S 2– средневзвешенная из дисперсий исходных выборок.
Таким образом, дисперсия суммы (или разности) независимых случайных величин равна сумме дисперсий этих величин.
В общем случае,
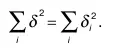
9. Закон распределения Пуассона и Гаусса
Закон Пуассона. Другое название его – закон ра-определения редких событий. Закон Пуассона (З. П.) применяется в тех случаях, когда маловероятно, и поэтому применение Б/З/Р нецелесообразно.
Достоинствами закона являются: удобство при вычислении, возможность вычислить вероятность в заданном промежутке времени, возможность замены времени другой непрерывной величиной, например, линейными размерами.
Закон Пуассона имеет следующий вид:
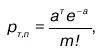
и читается следующим образом: вероятность появления события А в m раз при n независимых испытаниях выражается формулой вида (59), где а = пр – среднее значение p(A), причем а является единственным параметром в законе Пуассона.
Читать дальше
Конец ознакомительного отрывка
Купить книгу