Журнал «Юный техник» - Юный техник, 2012 № 09

Если теперь вы положите на конец короткой стороны линейки груз в 500 г, то на длинный конец достаточно положить гирьку или иной груз в 50 г, чтобы наши импровизированные весы застыли в равновесии.

Обоснуйте, почему так получается.

И, наконец, еще один опыт мы вам советуем провести уже на улице. Подсуньте нижний конец прочной трубы под камень и попробуйте приподнять его край, двигая верхний длинный конец лома или трубы вверх.

А теперь попробуйте проделать то же самое, подложив под трубу у самого камня кусок твердого дерева или другой камень — поменьше и двигая длинный конец лома вниз.

В каком случае приподнять оказалось камень легче?

Подумайте почему…

Вполне может быть, что ваше мнение и мнение вашего приятеля окажутся не одинаковы. Попробуйте разобраться, почему так получилось.

Почему водомерка не тонет? Может ли плавать иголка? Зачем при стирке поверхностно-активные вещества? Все дело в поверхностном натяжении жидкости. Слово итальянскому популяризатору науки Дж. Карбони и американскому литератору Л. Стюарту.

Для начала несколько слов о том, что такое поверхностное натяжение. Молекула жидкости обладает свойством притягивать к себе молекулы, которые ее окружают. Для тех молекул, что находятся внутри жидкости, равнодействующая всех этих сил равна нулю, и все они находятся в равновесии.

А вот молекулы на поверхности воды испытывают притяжение снизу и сбоку, а сверху у них лишь воздух. Появляется некая сила, направленная внутрь жидкости. В свою очередь, сила сплоченности между молекулами дает некий вектор, направленный по касательной к поверхности.

Проще говоря, поверхность жидкости ведет себя, как упругая мембрана. По ней и бегают водомерки, которые настолько малы и легки, что вода держит их, словно лед. Что такое силы поверхностного натяжения, нам помогут понять эксперименты.

Благодаря поверхностному натяжению по воде бегают водомерки и ящерицы-василиски.

ПЛАВАЮЩАЯ ИГЛА

Если бросить в воду обычную швейную иглу, она тут же утонет. А вот если мы немного схитрим, то можем заставить стальную иголку плавать.

Для этого нужно положить на воду листок папиросной бумаги, а на него — иголку. Сначала она будет плавать на листке бумаги, словно на плоту. Но постепенно бумага намокнет и утонет. А вот иголка останется на поверхности.

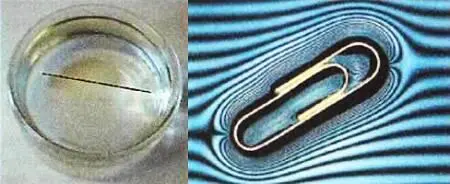
Кроме иголки, можно заставить плавать и скрепки.

ИЗМЕРЕНИЕ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ

Ясно, что поверхностное натяжение имеет определенную величину, а потому и не может держать особо большой груз. Но какова эта сила?

Теория гласит, что поверхностное натяжение ( Т) определяется силой ( F), поделенной на удвоенную площадь ( W) мембраны: T = F/2W. Двойка в этой формуле появляется потому, что поверхностный слой имеет две границы — верхнюю и нижнюю.

Практически силу поверхностного натяжения можно определить с помощью маленьких лабораторных весов, которые представляют собой две чашки, подвешенные на нитях к коромыслу.

Опустите одну чашу на поверхность воды в миске или чашке, а на другую осторожно начинайте помещать по одной малюсенькой гирьке до тех пор, пока другая чашка не оторвется от поверхности воды.

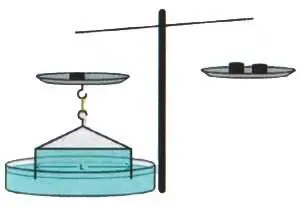
Эксперимент с весами.

Для справки: значение поверхностного натяжения дистиллированной воды 7,42 г/кв. м при 20 °C; для этилового спирта это значение равно 2,27 г/кв. м при той же температуре.

Добавьте в воду немного жидкости для мытья посуды или мыла, и вы увидите, что величина поверхностного натяжения стала меньше. Это и позволяет стирать белье, поскольку поверхностно-активные вещества, содержащиеся в мыльном растворе, ослабляют связь частиц грязи с нитями тканей.

Другой метод измерения поверхностного натяжения позволяет обойтись без весов. Один конец отрезка нержавеющей проволоки диаметром 1…2 мм и длиной около 20 см сверните в кольцо диаметром 3…4 см. Согните оставшуюся часть проволоки буквой U. Опустите кольцо прямо на поверхность жидкости, натяжение которой вы хотите определить. Добавляйте грузик или перемещайте массивный ползунок на противоположный конец проволоки, пока кольцо не оторвется от жидкости. Поверхностное натяжение (Т) жидкости будет определяться силой отрыва (F), поделенной на удвоенную длину окружности кольца, поскольку приходится учитывать и внутренний, и внешний обводы кольца.