Рудольф Сворень - Ваш радиоприемник

Простая логика подсказывает, что чем меньше потери, то есть, чем выше добротность системы, тем дольше существуют колебания в ней, тем медленнее они затухают (рис. 25, в, г).

Ну и, наконец, еще два замечания, теперь уже относительно самого хода колебаний. Прежде всего отметим, что в простейшей колебательной системе график, описывающий ход процесса, скажем, отклонение маятника от средней линии или изменение его скорости — это почти синусоида. Чем меньше потери, тем меньшее значение имеет это «почти». Сказанное относится к любым простейшим системам — механическим, тепловым, химическим, электромагнитным. Подобная универсальность синусоиды совсем не случайна, связана она с рядом особых математических свойств этой гармоничной кривой.

Время, в течение которого происходит полный цикл колебании , называется периодом , а число периодов за секунду — частотой .

Обе эти величины зависят от скорости колебательного процесса, от того, насколько быстро накопители обмениваются энергией, то есть, в конечном итоге, зависят от свойств, или, как принято говорить, от параметров этих накопителей. К примеру, частота колебаний струны зависит от ее упругости и массы. Чем массивнее струна, тем медленнее она набирает и сбрасывает скорость, тем меньше частота. Понижается частота и при уменьшении упругости, струна становится более вялой, она медленнее накапливает и отдает потенциальную энергию упругой деформации. Обе эти зависимости прекрасно иллюстрирует гитара — чем массивней, толще ее струна, тем медленней ее колебания, тем ниже частота звука. Кроме того, частота колебаний любой струны уменьшается, если ослабить ее натяжение, снизить упругость. Подобная зависимость частоты от параметров системы так же является универсальной и относится ко всем без исключения видам колебаний.

Начатый рассказ о колебательных процессах можно было бы продолжить, вспомнив о многих интересных системах, например, о периодических колебаниях планет, о многочисленных колебательных процессах в микромире, о сложных колебаниях, определяющих ритмы работы головного мозга, о гипотезе пульсирующей Вселенной. Однако, на все это у нас, к сожалению, нет времени. Нас ждет, то, из-за чего, собственно говоря, и был начат разговор о колебаниях. Нас ждет важнейшая электрическая цепь, без которой не обходится ни одни настоящий радиоприемник. Нас ждет знакомство с колебательным контуром.

Соединим конденсатор с катушкой индуктивности и введем в эту цепь — именно она и называется колебательным контуром — некоторое количество энергии. Сделать это можно двумя способами — зарядить конденсатор и таким образом создать в нем электрическое поле или же создать магнитное поле в катушке, пропустив через нее постоянный ток. В обоих случаях результат будет один — в системе начнутся электромагнитные колебания.

Допустим, энергия поступила в конденсатор (рис. 26).

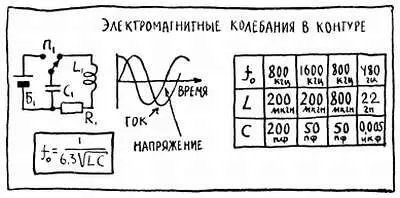
Рис. 26

Стремясь к устойчивому состоянию, он разряжается, в цепи идет ток, и в катушке возникает магнитное поле. Ток не прекратится и после полного разряда конденсатора. Теперь уже двигать заряды будет убывающее магнитное поле — как и при всяком изменении магнитного поля, на катушке будет наведена э. д. с. самоиндукции, которая и поддержит ток в цепи. В результате заряды опять будут накапливаться на обкладках конденсатора и он опять окажется в неустойчивом состоянии, опять окажется заряженным, правда, теперь уже в противоположной полярности. Когда магнитное поле исчезнет, все повторится сначала — разряд конденсатора, ток, магнитное поле катушки — и снова перезарядка конденсатора. Таким образом и будет непрерывно происходить обмен энергией между двумя накопителями — конденсатором и катушкой… В результате этого обмена в цепи будет протекать переменный ток и на каждом из ее элементов будет действовать переменное напряжение.

Все это очень напоминает колебания струны — ее упругость можно сравнить с емкостью конденсатора, а массу — с индуктивностью катушки. Обмен же энергией электрического и магнитного поля в точности напоминает обмен потенциальной и кинетической энергией при механических колебаниях.

* * *

ВОЛЬТМЕТР БЕЗ СТРЕЛКИ

Для начала вспомним один эпизод из чаплинского фильма «Малыш». Бедняга Чарли долго терпит издевательства распущенного мальчишки, пытается не обращать на него внимания и даже улыбается. Но вот чаша терпения переполнена. Чарли вспыхивает, и на сорванца обрушивается вполне заслуженное наказание.