Рудольф Сворень - Ваш радиоприемник

Приведенная схема, если ее использовать в детекторе, может легко отделить высокочастотную составляющую в том случае, когда сигнал не модулирован. А что будет во время модуляции? В этом случае у нас уже появляются две переменные составляющие — низкочастотная и высокочастотная. А вот как их разделить? И эту задачу можно решить с помощью RC -фильтров, но уже более сложных (рис. 23).

Под действием переменного напряжения через конденсатор проходит переменный ток. Ну а какова величина этого тока? От чего она зависит? Ответ на этот вопрос дает закон Ома для цепи переменного тока, очень похожий на закон, который мы вывели для тока постоянного. Основное отличие состоит в том, что вместо хорошо знакомого нам сопротивления появляется так называемое емкостное сопротивление конденсатора, обозначаемое х с (рис. 21, е). Оно так же, как и R , измеряется в омах, так же устанавливает связь между током и напряжением, однако емкостное сопротивление связано совсем с другими физическими процессами и поэтому имеет совсем другой смысл.

Прежде чем говорить подробно о емкостном сопротивлении, напомним еще раз, что такое величина, или, как еще говорят, сила тока. Величина тока показывает количество зарядов, которое проходит через какой-нибудь участок цепи за единицу времени. Чем быстрее движутся заряды, чем более массовый характер носит их движение, тем больше ток.

Теперь можно без долгих пояснений сказать, что величина тока в цепи с конденсатором, зависит от его емкости. Чем больше емкость, тем больше зарядов участвует в зарядном и разрядном токе. Однако это еще не все. В определении величины тока четко сказано, что мы учитываем не общее количество зарядов, проходящих мимо условного контрольного пункта, а количество, которое приходится на единицу времени. Отсюда следует, что величина тока в цепи с конденсатором зависит еще и от частоты самого тока. При изменении частоты количество движущихся зарядов не меняется, но зато они быстрее или медленнее совершают цикл заряд — разряд. Так, например, с увеличением частоты ток в цепи с конденсатором растет.

Если все эти рассуждения отнести к емкостному сопротивлению, то получится, что с увеличением емкости и частоты это сопротивление уменьшается. Конденсатор лучше пропускает тот ток, который имеет более высокую частоту. И дальше, для тока одной и той же частоты меньшее сопротивление будет сказывать конденсатор с большей емкостью (рис. 21, е). Вот теперь давайте посмотрим на реальную, хотя и не окончательную схему детектора (рис. 23, и).

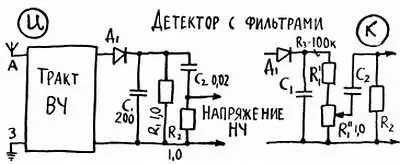
Рис. 23. и, к

Из «черного ящика» — в него мы пока поместили все, что находится между антенной и детектором — выводится высокочастотное модулированное напряжение. Оно подводится к детекторному узлу, или, как еще говорят, к детекторному каскаду, в который, как обычно, входит диод Д 1 и три фильтрующие цепи. По одной из них через сопротивление R 1 проходит постоянная составляющая продетектированного сигнала. Другого пути для этой составляющей нет, так как в каждой из двух остальных цепей имеется конденсатор — препятствие для постоянного тока непреодолимое.

Высокочастотная составляющая пройдет через конденсатор С 1 . Несмотря на сравнительно небольшую емкость этот конденсатор не представляет заметного сопротивления для высокочастотного тока — мы только на предыдущей странице отметили, что емкостное сопротивление уменьшается с увеличением частоты. Высокочастотная составляющая могла бы еще легче пройти через конденсатор С 2 , емкость которого во много раз больше, а емкостное сопротивление, следовательно, во столько же раз меньше, чем у C 1 . Однако последовательно с С 2 включено большое сопротивление R 2 и поэтому общее сопротивление цепи R 2C 2 для высокочастотного тока оказывается больше, чем емкостное сопротивление конденсатора C 1 .

Теперь попробуем выяснить, куда направится низкочастотная составляющая. Через C 1 она не пойдет — слишком мала емкость этого конденсатора и поэтому слишком велико его сопротивление для низкочастотного тока. Сравнительно легко пройдет низкочастотная составляющая по цепи R 2C 2 (даже на низких частотах конденсатор С 2 благодаря значительной емкости не оказывает заметного сопротивления), а также частично по сопротивлению R 1 . Ответвление низкочастотного тока в сопротивление R 1 это своего рода потери, но с ними можно мириться. Главная же задача решена нами без всяких скидок и абсолютно точно — мы разделили высокочастотный модулированный пульсирующий ток на три составляющие и одну из них, а именно низкочастотную, выделили в чистом виде, без примесей. Проходя по R 2 , переменный ток низкой частоты создаст на этом сопротивлении такое же по частоте и форме кривой низкочастотное напряжение, которое мы в итоге направим к громкоговорителю.