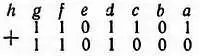Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Н. — Для начала я постараюсь не попасть в поставленную тобой ловушку и не скажу, что это один миллион сто одна тысяча сто один. А теперь я начну справа, полагая, что так легче справиться с поставленной задачей. Написанное число, как мы видим, содержит единицу, но оно не содержит основания, потому что его вторая справа цифра нуль; в то же время число содержит основание в квадрате, т. е. 4, и основание в кубе, потому что и третья и четвертая справа цифры — единицы. Затем можно сказать, что число не содержит основания в четвертой степени (это выражение равно 16), но содержит основание в пятой степени (т. е. 32) и основание в шестой степени (т. е. 64). Следовательно, написанное тобою число равно сумме названных чисел, а именно 64, 32, 8, 4 и 1; и на десятичном языке его следует назвать 109.

Л. — Превосходно, Незнайкин, ты прекрасно преобразовал это число. А сможешь ли ты теперь сделать сложение по правилам двоичной арифметики?

Н. — Вероятно, это довольно сложно, но я тем не менее готов попробовать.

Л. — Хорошо, вот тебе числа для сложения

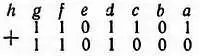
Для облегчения твоей работы я над каждой колонкой расположил маленькие буковки: а обозначает единицы, b — двойки, с — четверки, d — восьмерки, е — шестнадцатки (прости мне этот неологизм, несколько напоминающий десятки), f — тридцать-двойки, g — шестьдесят-четверки и h — сто-двадцать-восьмерки. Теперь можно начинать [20] Двоичная и десятичная системы счисления относятся к так называемым позиционным системам счисления, в которых цифры имеют различные значения в зависимости от того, на каком месте в записи числа они стоят. Существуют непозиционные системы счисления, как, например, римские цифры. В этой системе смысл каждого символа не зависит от его местоположения в записи числа: L = (50) 10 , С = (100) 10 , V = (5) 10 , LXXVI = 76. ( Прим. ред .) .

Н. — Возьмусь за дело. Предполагаю, что здесь поступают, как в десятичной арифметике. Не так ли?

Л. — Совершенно верно, только в двоичной арифметике элементарное сложение цифр производится по другим правилам.

Н. — Так, смело вперед. В колонке единиц, обозначенной буквой а , мы имеем 1 вверху и нуль внизу. Я естественно предполагаю, что нуль плюс 1 дает 1 и записываю полученный результат под чертой. Правильно?

Л. — Очень хорошо, но сознайся, что этот случай был не очень сложным.

Н. — Охотно признаю, а теперь перейдем к обозначенной буквой b колонке двоек. Это сложение меня несколько смущает, в обоих числах здесь стоят нули.

Л. — Но это самый классический случай, он настолько прост, что проще не бывает. Какой бы арифметикой мы ни занимались, для меня нуль плюс нуль всегда дает нуль.

Н. — Очень логично, об этом следовало бы подумать. Итак, в сумме на месте двоек я записываю нуль. Переходим к четверкам, обозначенным буквой с . Здесь тоже нет ничего трудного: 1 вверху и нуль внизу дают в сумме 1, что и записываю под чертой. С восьмерками дело обстоит чуточку посложнее; вверху у нас 1 и внизу тоже 1, их сумма 2, а у меня нет цифры 2, чтобы записать полученный результат.

Л. — Действительно, у тебя нет цифры 2, но ты можешь записать число 2 в двоичной системе в виде 1, за которой следует нуль. Иначе говоря, ты оказался в таком же положении, как при сложении по правилам десятичной арифметики, когда полученный результат превышает 10. Как ты обычно поступаешь в таком случае?

Н. — В таком случае я просто-напросто записываю цифру единиц и запоминаю цифру десятков.

Л. — Хорошо, так запиши цифру единиц, т. е. нуль в колонку d , и запомни цифру двоек, в нашем случае 1, которую ты потом прибавишь к сумме, полученной в колонке е .

Н. — Продолжим; в колонке е все обходится без каких бы то ни было трудностей; нуль в одном слагаемом, нуль в другом слагаемом да запомненная 1 дают в сумме только 1. Этот результат я и вписываю под чертой в колонке е . В колонке f мы сталкиваемся с уже знакомым положением: 1 + 1 дают в сумме 2 — я записываю нуль и запоминаю 1, которую предстоит прибавить к результату, полученному в колонке g . А вот с колонкой g справиться значительно труднее, потому что там мы имеем три слагаемых и каждое из них равно 1.

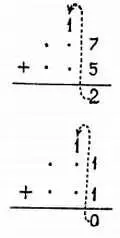
Л. — Но тебе надлежит применить этот же самый принцип. Сложение трех чисел по 1 в сумме дают 3, а это число в двоичной системе счисления записывается как одна двойка и одна единица, т. е. 1, после которой следует 1. Следовательно, запишешь 1 в колонку g и запомнишь 1.