Пауль Хоровиц - Искусство схемотехники. Том 2 [Изд.4-е]

Термин «шум» применяется ко всему тому, что маскирует полезный сигнал, поэтому шумом может оказаться какой-нибудь другой сигнал («помеха»); но чаще всего этот термин означает «случайный» шум физической (чаще всего тепловой) природы. Шум характеризуется своим частотным спектром, распределением амплитуд и источником (происхождением). Мы назовем основных «возмутителей спокойствия».

Джонсоновский шум.Любой резистор на плате генерирует на своих выводах некоторое напряжение шума, известное как «шум Джонсона» (тепловой шум). У него горизонтальный частотный спектр, т. е. одинаковая мощность шума на всех частотах (разумеется, до некоторого предела). Шум с горизонтальным спектром называют «белым шумом». Реальное напряжение шума в незамкнутой цепи, порожденное сопротивлением R , находящимся при температуре Т , выражается формулой

U ш. эфф= U шR= (4k TRB) 1/2,

где k — постоянная Больцмана, Т — абсолютная температура в Кельвинах ( К = °С + 273,16), B — полоса частот в Гц.

Таким образом, U ш. эфф — это то, что получится на выходе совершенно бесшумного фильтра с полосой пропускания В , если подать на его вход напряжение, порожденное резистором при температуре Т . При комнатной температуре (68 ° F = 20° С = 293К)

4k Т= 1,62·10 -20 В 2/(ГцОм),

(4k TR) 1/2= 1,27·10 -10 R 1/2В/Гц 1/2 = 1,27·10 -4 R 1/2В/Гц 1/2.

Например, резистор на 10 кОм при комнатной температуре имеет среднеквадратичное напряжение шума в разомкнутой цепи порядка 1,3 мкВ, измеренное в полосе 10 кГц (измерять можно, например, подсоединив резистор ко входу высококачественного усилителя и наблюдая напряжение на выходе усилителя вольтметром). Сопротивление источника этого напряжения шума равно просто R . На рис. 7.38 дан график простой зависимости плотности напряжения шума Джонсона (среднеквадратичное напряжение на корень квадратный из ширины полосы) от сопротивления источника.

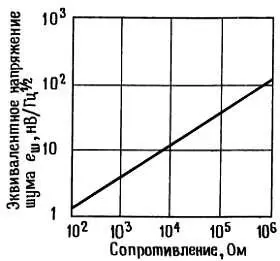
Рис. 7.38. Зависимость напряжения теплового шума от сопротивления.

Амплитуда напряжения шума Джонсона, вообще говоря, в данный конкретный момент непредсказуема, но она подчиняется закону распределения Гаусса (рис. 7.39), где p ( U ) dU — вероятность того, что мгновенное значение напряжения заключено между U и U + dU , а U ш — определенное выше среднеквадратичное (эффективное) напряжение шума.

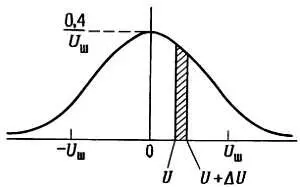
Рис. 7.39. p ( U, U+ dU) = (1/ U ш√(2π))e -( U^2/ U ш^2)dU, где U шесть эффективный шум. Площадь заштрихованной области равна вероятности нахождения мгновенного значения напряжения между Uи U+ ΔU.

Шум Джонсона устанавливает нижнюю границу напряжения шумов любого детектора, источника сигнала или усилителя, имеющего резистивные элементы. Активная составляющая полного сопротивления источника порождает шум Джонсона; так же действуют резисторы цепей смещения и нагрузки усилителя. Скоро мы увидим, как это происходит.

Интересно отметить, что любой физический аналог сопротивления (любой механизм потерь энергии в физической системе, например, вязкое трение малых частиц жидкости) имеет связанные с ним флуктуации соответствующей физической величины (в приведенном примере — это флуктуации скоростей частиц, проявляющиеся как хаотическое броуновское движение). Шум Джонсона — это просто специальный случай такого флуктуационно-диссипативного явления.

Шум Джонсона не следует путать с дополнительным шумовым напряжением, который возникает из-за эффекта флуктуации сопротивления, когда приложенный извне ток проходит через резистор. Этот «избыточный шум» имеет спектр приблизительно 1/ f , и он сильно зависит от конкретной конструкции резистора. Мы об этом поговорим позже.

Дробовой шум.Электрический ток представляет собой движение дискретных зарядов, а не плавно непрерывное течение. Конечность (квантованность) заряда приводит к статистическим флуктуациям тока. Если заряды действуют независимо друг от друга, то флуктуирующий ток определяется формулой

I ш. эфф= I шR= (2q I =B) 1/2,