Пауль Хоровиц - Искусство схемотехники. Том 1 [Изд.4-е]

Мы приступаем к рассмотрению делителя напряжения, который используется в электронных схемах весьма широко. В любой настоящей схеме можно найти не меньше полдюжины делителей напряжения. Простейший делитель напряжения — это схема, которая для данного напряжения на входе создает на выходе напряжение, которое является некоторой частью входного. Простейший делитель представлен на рис. 1.5.

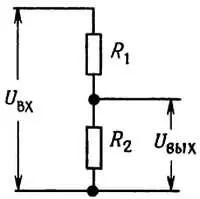
Рис. 1.5. Делитель напряжения. Приложенное напряжение U вхсоздает на выходе напряжение U вых(меньшее приложенного).

Что такое U вых ? Предположим здесь и далее, что нагрузки на выходе нет, тогда ток определяется следующим образом:

I= U вх/( R 1+ R 2)

(Мы воспользовались формулой для определения сопротивления резистора и правилом для последовательного соединения резисторов). Тогда для R 2

U вых= I· R 2= U вхR 2/( R 1 + R 2).

Обратите внимание, что выходное напряжение всегда меньше входного (или равно ему); поэтому мы говорим о делителе напряжения. Если одно из сопротивлений будет отрицательным, то можно получить усиление (т. е. выходное напряжение будет больше входного). Эта идея не так невероятна, как кажется на первый взгляд: вполне можно сделать устройство с отрицательными «приращениями» сопротивления (в качестве примера может служить туннельный диод) или просто с настоящим отрицательным сопротивлением (например, преобразователь с отрицательным импедансом, о котором мы поговорим позже). Однако эти примеры достаточно специфичны и не должны занимать сейчас ваше внимание.

Делители напряжения часто используют в схемах для того, чтобы получить заданное напряжение из большего постоянного (или переменного) напряжения.

Например, если в качестве R 2 взять резистор с регулируемым сопротивлением (рис. 1.6, а ), то мы получим не что иное, как схему с управляемым выходом; более простым путем комбинацию R 1R 2 можно получить, если у вас есть один резистор с переменным сопротивлением, или потенциометр (рис. 1.6, б ).

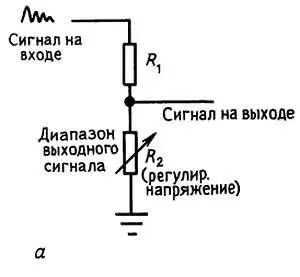
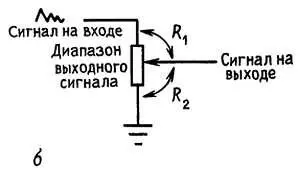
Рис. 1.6. Регулируемый делитель напряжения может состоять из двух резисторов — с фиксированным сопротивлением и с переменным сопротивлением, или из потенциометра.

Простой делитель напряжения играет важную роль и в тот момент, когда вы задумываете схему: входное напряжение и сопротивление верхней части резистора могут представлять собой, скажем, выход усилителя, а сопротивление нижней части резистора — вход последующего каскада. В этом случае, воспользовавшись уравнением для делителя напряжения, можно определить, что поступит на вход последнего каскада.

Все сказанное станет более понятным, когда чуть позже мы познакомим вас с одним интересным фактом (имеется в виду теорема об эквивалентном преобразовании схем). А сейчас немного отвлечемся от нашей темы и поговорим об источниках тока и напряжения.

Идеальный источник напряжения — это «черный ящик», имеющий два вывода, между которыми он поддерживает постоянное падение напряжения независимо от величины сопротивления нагрузки. Это означает, например, что он должен порождать ток, равный I= U/ R, если к выводам подключить резистор с сопротивлением R . Реальный источник напряжения не может дать ток, больший некоторого предельного максимального значения, и в общем случае он ведет себя как идеальный источник напряжения, к которому последовательно подключен резистор с небольшим сопротивлением. Очевидно, чем меньше сопротивление этого последовательно подключенного резистора, тем лучше. Например, стандартная щелочная батарея на 9 В в последовательном соединении с резистором, имеющим сопротивление 3 Ом, ведет себя как идеальный источник напряжения 9 В и дает максимальный ток (при замыкании накоротко) величиной 3 А (который, к сожалению, погубит батарею за несколько минут). По понятным причинам источник напряжения «предпочитает» нагрузку в виде разомкнутой цепи, а нагрузку в виде замкнутой цепи «недолюбливает». (Понятия «разомкнутая цепь» и «замкнутая цепь» очевидны: к разомкнутой цепи ничего не подключено, а в замкнутой цепи кусок провода замыкает выход.)