Ден Томел - Поиск неисправностей в электронике

Мы считаем в десятичной системе: от 0 до 9. Для представления следующей величины нам необходимо использовать вторую цифру, расположенную на одну позицию влево, которая представляет собой число, кратное 10, показывающее, сколько раз мы посчитали до десяти (от 0 до 9). Каждый раз, когда мы досчитали от 0 до 9, следующий разряд увеличивается на единицу (инкрементируется), а в младшем разряде опять появляется 0, свидетельствующий о переходе на новый десяток.

Двоичная система счисления работает точно так же. Символы 0 и 1 называются двоичными цифрами, или, для краткости, битами. После того, как последняя значащая цифра становится равной 1, она сбрасывается в 0, а следующий разряд слева инкрементируется, что представляет количество двоек в числе. Следующий разряд слева представляет количество четверок, следующий — восьмерок и т. д. С каждым разрядом число увеличивается вдвое (таб. 8.1).

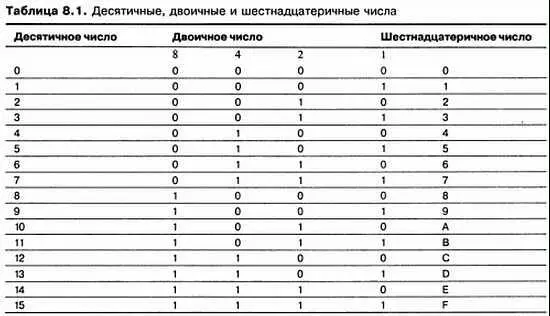
Сталкиваясь с большими двоичными числами, трудно отслеживать нули и единицы. Один из способов решения этой проблемы заключается в преобразовании двоичных чисел в десятичные с помощью сложения удельного веса разрядов, в которых находятся 1. Например:

8 4 2 1

1 1 0 1 - двоичное = 8 + 4 + 1 = 13 — десятичное

При больших двоичных числах такое преобразование становится сложным и порождает много ошибок. Более простой и распространенный способ представления больших двоичных чисел заключается в их преобразовании в шестнадцатеричную систему счисления.

Шестнадцатеричная система счисления использует 16 символов, поэтому она является системой с основанием 16. Первые 10 символов такие же, как в десятичной системе — от 0 до 9. Остальные 6 символов — это буквы от А до F, представляющие десятичные числа 10–15 соответственно.

Причина привлекательности шестнадцатеричной системы заключается в том, что преобразование чисел между ней и двоичной системами счисления выполняется очень просто. Для преобразования двоичного числа в шестнадцатеричное двоичное число делится на группы по 4 бита, начиная с наименее значимого бита (правого). Каждая группа из 4 битов затем непосредственно преобразуется в эквивалентный шестнадцатеричный символ, как указано в табл. 8.1. Приведенный ниже пример иллюстрирует типичное преобразование.

1010011101 — > 10 1001 1101 —> 29D

Шестнадцатеричная система счисления не меняет того факта, что цифровые системы работают с двоичными числами. Она просто упрощает нам обращение со значениями в двоичной системе. Гораздо проще использовать число 29D, чем 1010011101, при этом оба они представляют ту же величину. Более подробно с системами счисления и преобразованиями между ними вы можете познакомиться в любом из многих популярных изданий.

Базовые элементы, которые были рассмотрены в главе 7 , используются для построения более сложных комбинационных логических приборов, имеющих самую разную структуру, каждая их которых обладает собственными свойствами. Рассмотрим некоторые наиболее популярные и распространенные типы ИМС комбинационной логики.

Дешифраторы

Комбинационные приборы чаще всего выступают в качестве дешифраторов и шифраторов. Декодирование можно рассматривать как выявление соответствующего некоему условию входного двоичного сигнала с соответствующей реакцией на выходе. На рис. 8.1 показан элемент И-НЕ с четырьмя входами, который используется для декодирования величины 0В шестнадцатеричное (1011 двоичное).

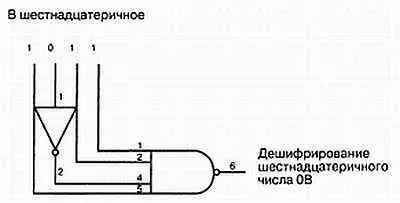
Рис. 8.1. Декодирование шестнадцатеричного числа ОВ

Выход этой схемы имеет уровень НИЗКИЙ только тогда, когда на его входах формируется двоичное число 1011 (шестнадцатеричное 0В). Любая другая комбинация битов на входах дает на выходе логический уровень ВЫСОКИЙ.

Множество типов дешифраторов с различными функциональными возможностями выпускаются в корпусах ИС. Очень популярен дешифратор «три на восемь» 74138 с двоичным входом на три разряда и 8 отдельных выходов с активным низким уровнем, а также три разрешающих входа, которые должны быть активированы для работы схемы (рис. 8.2).

Рис. 8.2. Дешифратор три на восемь 74138