Юрий Ревич - Занимательная микроэлектроника

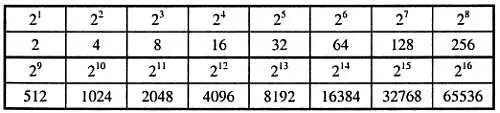
На первое время достаточно запомнить верхний ряд, остальное выучится позже само.

Сложнее переводить из десятичной системы в двоичную, в учебниках описывается устрашающая процедура, основанная на делении столбиком. Я сейчас попробую вам показать способ, который позволяет переводить числа в двоичную систему несколько более простым методом, причем небольшие числа можно преобразовать даже в уме. Это, в сущности, то же самое деление, но без излишних сложностей и формальностей. Запомните сначала следующее правило: число, равное какой-либо степени двойки, имеет 1 в разряде с номером, на единицу большим степени, остальные все нули:

2 1= 2 10=10 2;

2 2= 4 10= 100 2;

2 3= 8 10= 1000 2и т. д.

Способ состоит в следующем: пусть мы имеем, например, десятичное число 59. Подбираем наибольшую степень двойки из таблицы ранее, не превышающую этого числа: 32, что есть 5-я степень. Ставим 1 в шестом разряде: 100000. Вычитаем подобранную степень из исходного числа (59–32 = 27) и подбираем для остатка также степень, его не превышающую: 16 (2 4). Ставим единицу в 5-м разряде: 110000. Повторяем процедуру вычитания-подбора: 27–16 = 11, степень равна 8 (2 3), ставим единицу в 4-м разряде: 111000. Еще раз: 11 — 8 = 3, степень равна 2 (2 1), ставим единицу во 2-м разряде: 111010. Последнее вычитание дает 1, которую и ставим в младший разряд, окончательно получив 59 10= 111011 2. Если бы исходное число было четным, к примеру 58, то в последнем вычитании мы бы получили 0, и число в двоичной системе также оканчивалось бы на ноль: 58 10= 111010 2.

Кстати, полезно также обратить внимание, что числа, на единицу меньшие степени двойки, имеют количество разрядов, равное степени, и все эти разряды содержат единицы:

2 1— 1 = 1 10= 1 2;

2 2— 1 = 3 10= 11 2;

2 3— 1 = 7 10= 111 2;

Подобно тому, как наибольшее трехразрядное число в десятичной системе равно 999, и чисел таких всего 10 3= 1000 (от 000 до 999), в двоичной системе тех же трехразрядных чисел будет 2 3= 8 штук, в диапазоне от 000 до 111, т. е. от 0 до 7. Таким образом, наибольшее двоичное число с данным количеством разрядов будет всегда содержать все единицы во всех разрядах.

А вот из двоичной системы в шестнадцатеричную и обратно перевод очень прост: 16 есть 2 4и без всяких вычислений можно утверждать, что одноразрядное шестнадцатеричное число будет иметь ровно 4 двоичных разряда. Поэтому перевод из двоичной системы в шестнадцатеричную осуществляется так: двоичное число разбивается на т. н. тетрады, т. е. группы по четыре разряда, а затем каждая тетрада переводится отдельно и результаты выписываются в том же порядке. Так как в тетраде всего 16 вариантов, то их опять же легко выучить наизусть:

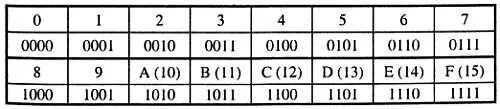
Например, число 59 10, т. е. 0011 1011 2, будет равно 3Bh.

Точно так же осуществляется и обратный перевод — каждое шестнадцатеричное число просто записывается в виде совокупности тетрад. Так, число A2FC 16выразится, как 1010 0010 1111 1100 2. Заметьте, что пробелы между тетрадами введены просто для удобства восприятия, подобно пробелам между тройками разрядов (классами) в записи больших десятичных чисел, и никакой иной нагрузки не несут. При записи двоичных чисел в тексте программ, как ассемблерных, так и программ на языках высокого уровня, естественно, эти пробелы ставить запрещается.

В качестве упражнения можете поразмыслить над вопросом, как переводить числа из двоичной в восьмеричную и четверичную системы, и наоборот: если вы справитесь с этим самостоятельно, считайте, что вы все поняли насчет систем счисления, применяемых в электронике.

Байты

Слово байт (byte) создано искусственно и представляет собой сокращение от BinarY digiT Eight, что буквально переводится, как «двоичная цифра восемь». На самом деле байт — это просто восьмиразрядное двоичное число. Соответственно, он имеет ровно два шестнадцатеричных разряда, или две двоичных тетрады. Такой байт был введен фирмой IBM в конце 50-х годов прошлого века, до этого (а в СССР — вплоть до 1969 года) применялись байты с другим количеством разрядов (5, 6 и 7).

Почему именно 8 разрядов? Да просто потому, что так удобно: число кратно степени двойки, т. е. легко масштабируется, скажем, шестнадцатиразрядное число — просто два байта, записанные подряд, подобно тетрадам в самом байте. В то же время оно относительно невелико и одновременно достаточно емко: имеет 256 значений, которых с лихвой хватает, к примеру, для представления всех печатных знаков европейских алфавитов (во всяком случае, до нашествия фирмы Microsoft с ее системой Windows хватало — что, конечно же, следует рассматривать, как шутку).