В Бессонов - Радиоэлектроника для начинающих (и не только)

Отсюда получаем: R 0= R1∙ R2/( R1+ R2). (2.10, б )

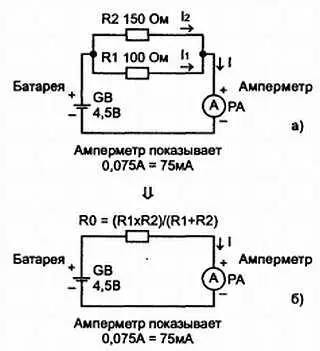
Рис. 2.19. Из которого можно сделать вывод, что при параллельном соединении резисторов общее сопротивление цепи меньше наименьшего сопротивления одного из резисторов цепи

Для трех параллельно соединенных резисторов:

1/ R 0= 1/ R1+ 1/ R2+ 1/R3(2.10, в )

А теперь включите миллиамперметр в цепь первого резистора (рис. 2.20, а ), верхний предел должен быть примерно 50 мА. Когда подключите все элементы схемы, подключите батарею. Прибор покажет силу тока I1 = 45 мА. Отключите батарею и подключите миллиамперметр в цепь второго резистора (рис. 2.20, б ). Подключите батарею и замерьте силу тока: прибор покажет I2 = 30 мА.

А теперь сравните все три показания миллиамперметра: сумма сил токов через резисторы R1 и R2 равна силе тока в общей цепи (силе тока, потребляемой от батареи). Отсюда вывод, при параллельном соединении резисторов сила тока в общей (неразветвленной) цепи равна сумме сил токов, протекающих через резисторы.

I 0= I1+ I2. (2.11, а )

Если параллельно соединены три резистора, тогда:

I 0= I1+ I2 + I3 . (2.11, б )

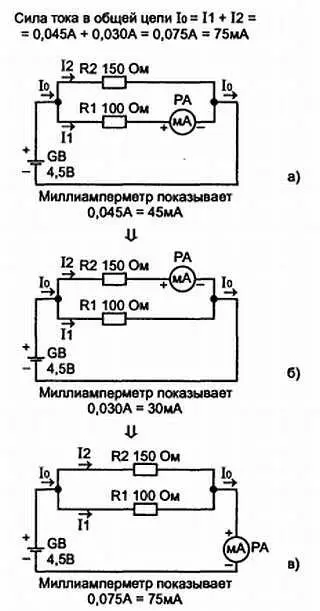
Рис. 2.20. Из которого можно сделать вывод, что сумма силы токов в ветвях (при параллельном соединении) равна силе тока, потребляемого от источника (силе тока в неразветвленной части цепи)

Теперь переключите прибор для измерения напряжения, соберите схему, как показано на рис. 2.21, и замерьте напряжение вначале на резисторе R1, затем на резисторе R2. Вы убедились, что вольтметр в обоих случаях показывает одно и то же напряжение, равное напряжению на зажимах батареи, т. е. 4,5 В? Отсюда вывод: при параллельном соединении резисторов падения напряжения на них равны.

U1 = U2. (2.12, а )

Для трех параллельно соединенных резисторов

U1= U2= U3. (2.12, б )

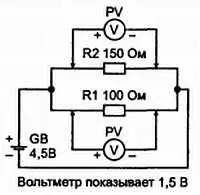
Рис. 2.21. Который позволяет быстро определить, что при параллельном соединении резисторов напряжение на них одинаковое

Часто в вашей практике (при изготовлении какого-либо прибора, устройства) встречаются или могут встретиться такие случаи, когда отсутствует резистор необходимого номинала. Есть два выхода из этого положения.

1. Найти два резистора, желательно одинакового номинала, чтобы сумма их сопротивлений была равна сопротивлению заменяемого резистора. Эти резисторы надо соединить последовательно (2.8).

2. Резисторы можно соединить и параллельно. Для этого следует подобрать один резистор R1, который образует вместе с другим параллельно соединенным резистором R2 заданное сопротивление R 0. Если учесть, что номинальные значения сопротивлений постоянных резисторов образуют не непрерывный ряд (смотри табл. 2.2), а в ваших запасах отсутствуют резисторы многих номиналов, входящих в шкалу номинальных значений, то задачу по отысканию второго резистора нельзя отнести к легким. Вы в этом скоро убедитесь. Ускорить и облегчить решение задачи по подбору второго резистора можно с помощью диаграммы, изображенной на рис. 2.22.

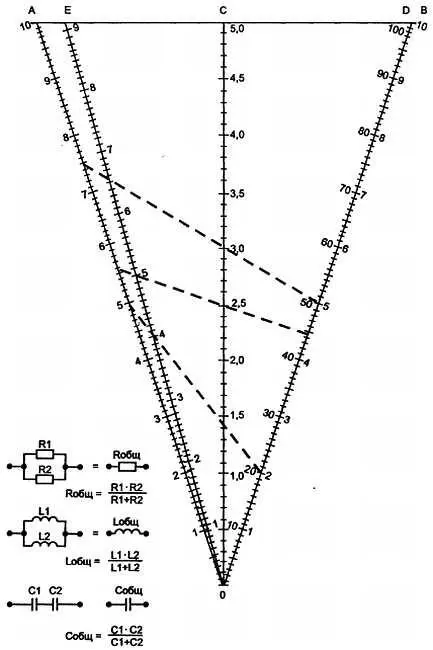
Рис. 2.22. Сетка для подбора второго резистора при параллельном соединении резисторов

С помощью этой номограммы можно определить электрические величины двух параллельно соединенных резисторов или катушек индуктивности, а также двух последовательно соединенных конденсаторов.

При определении электрических величин соединяемых резисторов, катушек индуктивности или конденсаторов сопротивления, индуктивности или емкости которых имеют один порядок, пользуются шкалами ОА, ОВ, ОС , а если их значения различаются на один порядок, то шкалами ОА, OD, ОЕ .

Пример 1. Параллельно соединены два резистора с номиналами 7,5 кОм и 5 кОм. Прикладывая край линейки к делениям 7,5 на шкале ОА и к 5 — на шкале ОВ , на шкале ОС считываем результат — 3. Общее с сопротивление резисторов будет 3 кОм.