Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Как уже говорилось, каждая из этих орбиталей имеет свою форму. Довольно часто орбитали называют в соответствии с их формой. Например, три различных 2 p -орбитали, вместо того чтобы обозначать их 2 p 1, 2 p 0и 2 p −1, называют 2 p x, 2 p zи 2 p y. Связь между этими индексами и формами прояснится, когда мы познакомимся с соответствующими формами.

На рис. 10.1 представлена диаграмма энергетических уровней атома водорода. Изображены уровни с n от 1 до 5. Для удобства восприятия масштаб интервалов не соблюдается, но, как и показано, с увеличением n интервал между уровнями становится меньше. Также с увеличением n возрастает число различных состояний (орбиталей), соответствующих конкретному значению n . Водород — это особый случай, поскольку у него имеется лишь один электрон. Для водорода все орбитали с одинаковым значением n обладают равной энергией. В следующей главе будет объяснено, что в атомах с несколькими электронами орбитали с разными значениями l при одном и том же n обладают разными энергиями.

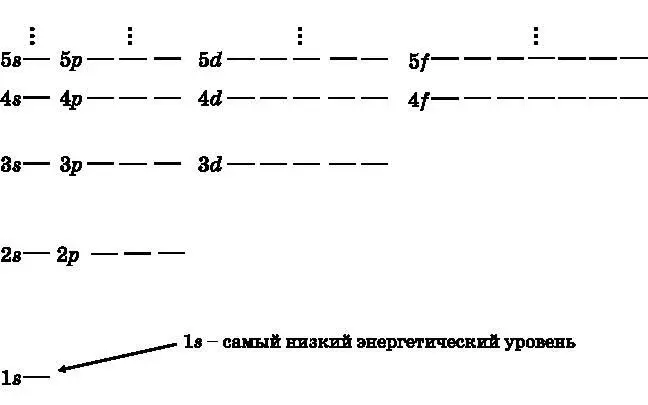
Рис. 10.1. Диаграмма энергетических уровней водорода. Изображены первые пять энергетических уровней. Для удобства восприятия масштаб интервалов между уровнями не соблюдается. Энергия зависит только от главного квантового числа n. Показано количество орбиталей каждого типа. При n = 4 имеется одна s-орбиталь, три разные p-орбитали, пять разных d-орбиталей и семь разных f-орбиталей {13} 13 На уровне n =5 не показаны девять g -орбиталей, соответствующих l =4. — Примеч. пер. . Диаграмму можно продолжить для n = 6. Различные уровни иногда называют оболочками

Хотя значения энергии в атоме водорода зависят только от главного квантового числа n , квантовые числа l и m тоже играют важную роль. Они определяют форму орбиталей и другие свойства, присущие атому водорода. Например, квантовое число m называется магнитным квантовым числом. Три 2 p -орбитали (2 p 1, 2 p 0и 2 p −1) различаются значениями квантового числа m . Когда атом водорода помещают в магнитное поле, энергии этих трёх орбиталей перестают быть одинаковыми.

Из диаграммы энергетических уровней, вычисленных с помощью уравнения Шрёдингера (см. рис. 10.1), становится ясно, как возникает эмпирическая диаграмма, представленная на рис. 9.3. Оптические переходы, видимые как линии в спектре атома водорода и описываемые формулой Ридберга, — это переходы между энергетическими уровнями атома водорода, энергии которых вычисляются на основе квантовой теории без каких-либо подгоночных параметров.

Как уже упоминалось, квантовые числа n, l и m вместе определяют формы волновых функций. Для s -орбиталей l =0. Это означает, что электрон не имеет углового момента {14} 14 Квантовое число l называется орбитальным и характеризует момент импульса электрона, называемый также угловым моментом. — Примеч. пер. в своём движении относительно ядра атома. Все направления выглядят равноценными, так что s -орбитали — это сферически симметричные трёхмерные волны амплитуды вероятности. На рис. 10.2 схематически показаны орбитали (волны амплитуды вероятности) 1 s , 2 s и 3 s . Более тёмный тон означает бо́льшую вероятность обнаружить электрон на соответствующем расстоянии от центра. Расстояния, на которых вероятности достигают максимума, показаны сплошными окружностями. Середины белых областей внутри орбиталей 2 s и 3 s (пунктирные окружности) — это узлы, то есть области, где вероятность обнаружить электрон обращается в нуль. При переходе от 1 s к 2 s и 3 s размеры орбиталей значительно возрастают. С увеличением квантового числа n повышается вероятность обнаружить электрон вдали от ядра.

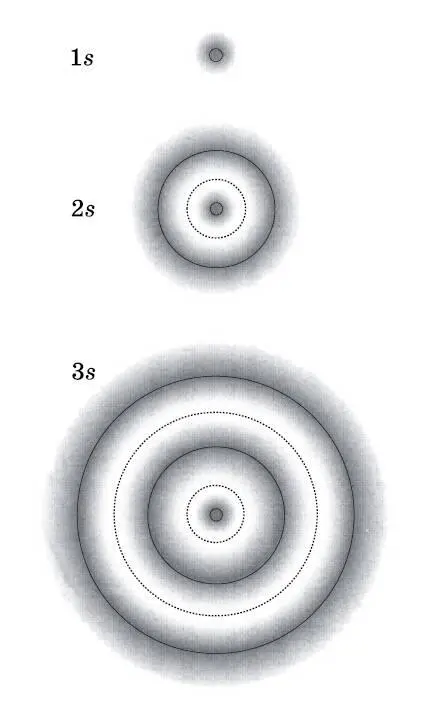
Рис. 10.2. Двумерные представления орбиталей 1 s, 2 s и 3 s. В действительности они сферические. Более тёмный тон соответствует более высокой вероятности обнаружения электрона. Сплошными окружностями обозначены максимальные значения этой вероятности. Пунктирные окружности — это узлы, где данная вероятность обращается в нуль. При данном способе изображения орбитали имеют довольно чёткую внешнюю границу. Орбитали — это волны, которые становятся очень малыми на больших расстояниях, но обращаются в нуль лишь тогда, когда расстояние от центра стремится к бесконечности