Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Энергии различных состояний атома водорода описываются единственным квантовым числом n . Однако в действительности есть четыре квантовых числа, связанных с электронами в атомах. Они появляются при решении задачи об атоме водорода в рамках квантовой теории. Одно из них существенно лишь для атомов и молекул, имеющих более одного электрона. В этом смысле атом водорода является частным случаем, поскольку в нём всего один электрон. Для атома водорода, помимо главного квантового числа n , есть ещё два квантовых числа — l и m . Число l называется орбитальным квантовым числом, m — магнитным квантовым числом. От них в сочетании с квантовым числом n зависит, сколько различных состояний связано с конкретным значением энергии, они также определяют форму волновых функций. Четвёртое квантовое число обозначается s . Его называют спи́новым квантовым числом.

Когда Бор решал задачу об атоме водорода, в рамках старой квантовой теории считалось, что электрон движется по орбитам, имеющим разные формы и значения энергии. Корректное квантовое решение Шрёдингера для атома водорода даёт энергетические уровни и волновые функции, которые соответствуют боровским орбитам и называются «орбиталями». Обсуждая атомы и молекулы, мы часто используем термины «волновая функция» и «орбиталь» в качестве синонимов. Орбитали являются волнами амплитуды вероятности, которые подчиняются принципу неопределённости Гейзенберга, чем отличаются от боровских орбит.

Как уже отмечалось выше, главное квантовое число n может принимать целочисленные значения n ≥1, то есть 1, 2, 3, 4 и так далее, а l может принимать значения от 0 до n −1 с целым шагом. Число m может иметь значения от l до − l с целым шагом. Наконец, число s может принимать только два значения: +½ и −½. Сводка возможных значений квантовых чисел приведена в таблице ниже.

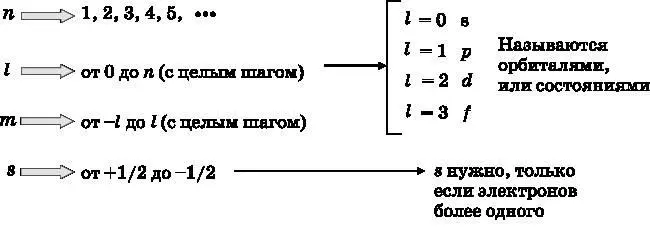
По историческим причинам состояния с различными значениями квантового числа l имеют индивидуальные обозначения. Состояние l =0 называется s -орбиталью. При l =1 говорят о p -орбитали, при l =2 — это d -орбиталь, а при l =3 — f -орбиталь. Для обсуждения всех атомов нам не понадобится заходить далее f -орбиталей, то есть l =3. Как показано ниже, различные орбитали имеют разные формы.

Поскольку энергии состояний (орбиталей) атома водорода зависят только от квантового числа n , для n >1 имеется более одного состояния с одинаковой энергией. Для n =1 имеем l =0 и m =0 (см. таблицу), поэтому существует единственная орбиталь с n =1. Для этой орбитали l =0, так что её обозначают как 1 s -орбиталь. Для n =2 число l может быть равно 0, что даёт 2s-орбиталь. Однако для n =2 число l также может равняться 1. При l =1 число m может быть равно 1, 0 или −1 (см. таблицу). При l =1 — это p -орбиталь, причём существуют три разные p -орбитали, обозначаемые 2 p 1, 2 p 0и 2 p −1. Здесь 2 — это главное квантовое число n, p означает l =1, а три индекса— это три возможных значения m . Таким образом, для n =2 существует четыре различных состояния.

Если n =3, то l может быть равно нулю, что даёт 3 s -орбиталь. Также l может быть равно 1, что при m = 1, 0 и −1 даёт орбитали 3 p 1, 3 p 0, и 3 p −1. Кроме того, l может быть равно 2. Для l =2 число m может иметь значения 2, 1, 0, −1 и −2. Это d -орбитали: 3 d 2, 3 d 1, 3 d 0, 3 d −1и 3 d −2. Всего имеется пять d -орбиталей. Таким образом, для n =3 имеется девять различных состояний: одна s -орбиталь, три p -орбитали и пять d -орбиталей. Когда n =4, есть 4 s -орбиталь, три различные 4 p -орбитали (4 p 1, 4 p 0и 4 p −1), пять различных 4 d -орбиталей (4 d 2, 4 d 1, 4 d 0, 4 d −1и 4 d −2). Дополнительно имеется семь f -орбиталей: 4 f 3, 4 f 2, 4 f 1, 4 f 0, 4 f −1, 4 f −2и 4 f −3. Таким образом, для n =4 имеется в общей сложности 16 состояний: одна s -орбиталь, три p -орбитали, пять d -орбиталей и семь f -орбиталей.