Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Давайте объединим эти формулы.

Первым делом возведём в квадрат величину p :

p 2= m 2∙ V 2.

Если теперь разделить обе части уравнения на 2 ∙ m , то в правой части получим кинетическую энергию

½ m ∙ V 2,

а в левой части —

p 2/2∙ m .

Отсюда следует выражение для кинетической энергии:

E = p 2/2 ∙m .

Используя соотношение де Бройля, можно получить выражение: p 2= h 2/ λ 2. Подставляя его в выражение для энергии, получаем:

E = h 2/2 ∙m∙λ 2.

Наконец, применим наше правило λ =2 L / n для возможных значений длины волны. Из него следует: λ 2=4 L 2/ n 2. Подставив это выражение в формулу для энергии, находим:

E = n 2 h 2/8 ∙m∙λ 2,

где n принимает любые целые значения: 1, 2, 3 и т. д. Целочисленная величина n называется квантовым числом.

Мы получили очень важный результат: значения энергии абсолютно малой частицы в абсолютно малом ящике. Этот результат очень тесно связан с поведением электронов в атомах и молекулах. Как видно из формулы, набор возможных значений энергии не непрерывен, поскольку n может принимать только целочисленные значения; другие величины, входящие в формулу, для конкретной системы являются константами. Мы будем говорить, что энергия квантуется, то есть она может принимать лишь некоторые значения, определяемые физическими свойствами системы и квантовым числом.

Существует дискретный набор энергетических уровней для данных значений массы m и размера ящика L . Поскольку квантовое число n принимает значения 1, 2, 3 и т. д., соответствующие значения энергии будут равны

h 2/8 ∙m∙L 2, 4∙ h 2/8 ∙m∙L 2, 9∙ h 2/8 ∙m∙L 2, и т. д.

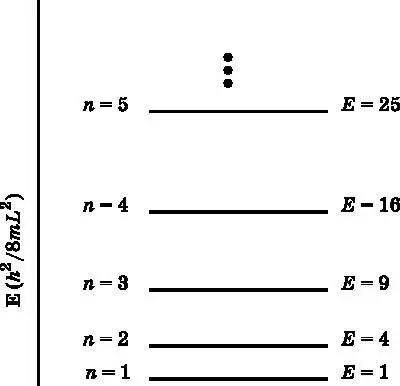
Рис. 8.6. Энергетические уровни частицы в ящике. Здесь n— квантовое число, а E— энергия, которая увеличивается как квадрат квантового числа. Энергия выражена в единицах h 2 /8 ∙ m∙L 2 , так что хорошо видно, как она возрастает. Штриховой линией обозначена нулевая энергия. Самый низкий энергетический уровень не совпадает с линией E = 0 в отличие от случая классической частицы в ящике

На рис. 8.6 представлена диаграмма энергетических уровней для первых нескольких значений энергии частицы в ящике. Энергия выражена в единицах h 2/8 ∙ m∙L 2. Чтобы получить фактическое значение энергии, нужно просто подставить конкретные значения m и L в формулу для энергетических уровней. На диаграмме видно, что энергия увеличивается как квадрат квантового числа n . Штриховой линией обозначено, где энергия равна нулю. Квантовая частица в ящике на наинизшем энергетическом уровне имеет ненулевую энергию, чем резко отличается от классической частицы в ящике. На классической ракетбольной площадке энергия, которой может обладать мяч, непрерывна. Ударяя по мячу чуть сильнее или чуть слабее, его энергию можно увеличить или уменьшить на любую величину. Однако в квантовом ракетболе возможны лишь отдельные значения энергии, показанные на рис. 8.6. Как отмечалось в начале нашего разговора о квантовой частице в ящике, наименьшая энергия не равна нулю. Если бы квантовая частица в ящике могла иметь нулевую энергию, это нарушало бы принцип неопределённости.

Частица в ящике — это очень простая иллюстрация общего свойства абсолютно малых систем. Энергия таких систем не обязательно непрерывна. Частица в ящике не является физически реализуемой системой, поскольку она одномерна и окружена «идеальными» стенками. Однако атомы и молекулы — реальные системы. Энергетические уровни атомов и молекул исследовались очень подробно, а их квантованные энергетические уровни измерялись экспериментально и рассчитывались теоретически. Подобно тому как энергетические уровни частицы в ящике зависят от свойств системы (массы частицы и длины ящика), энергетические уровни в атомах и молекулах зависят от свойств этих атомов и молекул.