Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

На рис. 8.3 показан (запрещённый) разрыв волновой функции внутри ящика. Волновая функция обозначена φ(греческая буква «фи»). По вертикальной оси отложена амплитуда волновой функции. Штриховой линией показан её нулевой уровень. Волновые функции, представляющие собой волны амплитуды вероятности, могут колебаться между положительными и отрицательными значениями. Волновая функция, представленная на рис. 8.3, имеет возле стенок значения, отличные от 0. Однако волновая функция должна быть нулевой вне ящика, то есть для значений x меньше 0 и больше L она должна быть равна нулю. На рисунке волновая функция неожиданно перескакивает от ненулевого значения у стенки внутри ящика к нулевому значению сразу за стенкой вне ящика. Таким образом, волновая функция, изображённая на рис. 8.3, не является допустимой, поскольку она не является непрерывной. Эта функция не может представлять квантовую частицу в ящике.

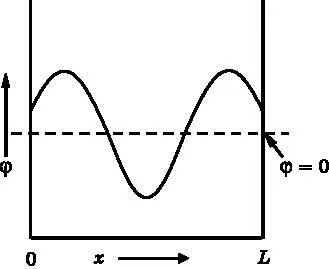
Рис. 8.3. Разрывная волновая функция внутри ящика. Волновая функция обозначена φ . По вертикальной оси отложена амплитуда волновой функции. Штриховой линией показано, где волновая функция обращается в нуль; это значение она должна иметь вне ящика. Волновая функция имеет ненулевое значение у стенок внутри ящика и затем должна скачкообразно (негладко) стать равной нулю вне ящика

Чтобы волновые функции, представляющие частицу в ящике, были физически приемлемыми, их значения у стенок должны быть нулевыми, и тогда они не будут испытывать разрыва на стенках. Выполнить это условие нетрудно. На рис. 3.1 показана волновая функция в свободном пространстве. Она колеблется между положительными и отрицательными значениями. Каждый раз, переходя от положительных значений к отрицательным или от отрицательных к положительным, она проходит через ноль. На самом деле нулевые точки отделены друг от друга половиной длины волны. Поэтому для получения хороших волновых функций частицы в ящике мы должны выбирать волны, длина которых позволяет им укладываться в ящике так, чтобы нулевые точки находились как раз на стенках.

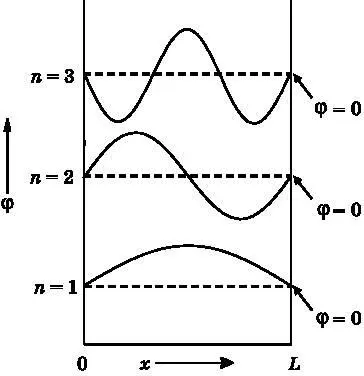
Рис. 8.4. Три примера волновых функций φ внутри ящика, которые являются непрерывными. Для ясности они сдвинуты друг относительно друга по вертикали. По вертикальной оси отложена амплитуда волновой функции. Штриховая линия показывает, где волновая функция равна нулю, что должно соблюдаться вне ящика. Волновые функции, имеющие нулевые значения на стенках, непрерывны на них

На рис. 8.4 приведены три примера волн, которые подходят на роль волновых функций для частицы в ящике. Нижняя из них обозначена n =1 и состоит из одной полуволны. Она начинается слева на амплитуде 0, проходит максимум и затем снова опускается до нуля на стенке в точке L . Следующая волна, расположенная выше и обозначенная n =2, состоит из одного полного колебания. Она тоже начинается у левой стенки на амплитуде 0, проходит положительный пик, возвращается к нулю, затем следует отрицательный пик и возвращение к нулю на стенке в точке L . Волна, обозначенная n =3, содержит полтора периода. Подходит любая волна, содержащая целое число полуволн, то есть 1, 2, 3, 4, 5 и так далее половин длины волны, и расположенная так, чтобы она начиналась на нуле слева и заканчивалась на нуле справа.

Величина n — это число полуволн конкретной волновой функции. При n =1 длина волны λ составляет 2 L , поскольку длина ящика равна L , а n =1 соответствует половине длины волны. При n =2 длина волны составляет L , поскольку ровно одна длина волны помещается между стенками. При n =3 между стенками помещаются три полуволны, то есть 1,5 λ = L . В этом случае λ = L /1,5, то есть λ =⅔ L . Обратите внимание, что здесь обнаруживается общее правило: λ =2 L / n , где n — целое число. Для n =1 получаем λ =2 L , для n =2 — λ =2 L /2, для n =3 — λ =⅔ L и т. д.