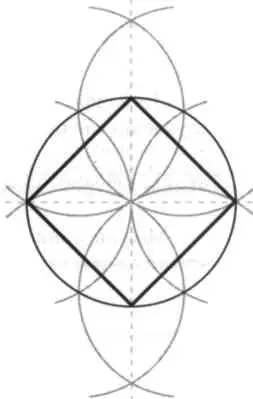
В книге Маскерони содержится знаменитая задача Наполеона (считается, что сам Наполеон предложил ее математику). Она состоит в том, чтобы в данной окружности определить вершины квадрата, используя только циркуль.
Если мы попробуем решить эту задачу простым сложением, а наклеек достаточно много, то на это уйдет слишком много времени, и ошибок не избежать, даже используя калькулятор. Лучше применить способ Эйлера и сложить только два слагаемых:
1 + 1/2 + 1/3 + ... + 1/n = γ + ln n.
ПОСТОЯННАЯ у И ПРОСТЫЕ ЧИСЛА
Постоянная у встречается гораздо реже, чем я или е. Несложно найти формулу, которая связывает все три постоянные:
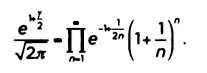
Сам Эйлер тоже нашел взаимосвязи между у и дзета-функцией:
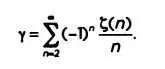
Существуют также формулы, связывающие напрямую ус простыми числами, как, например, формула Франца Мертенса (1840-1927):
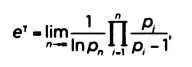
где р — простые числа. Таким образом, в ней задействованы у, дзета- функция и простые числа. Нет сомнений, что третья постоянная Эйлера имеет большое значение, которое со временем будет только возрастать.
Логарифм можно вычислить на калькуляторе, а γ в данном случае можно округлить до 50 знаков:
0,57721566490153286060651209008240243104215933593992...
Можно привести еще один, более абстрактный пример: чтобы узнать, сколько делителей п в среднем есть между 1 и n, можно использовать выражение In n + 2γ - 1. Это приближение становится тем точнее, чем больше значение я и чем больше у него делителей.
ФОРМУЛА ЭЙЛЕРА — МАКЛОРЕНА В ДЕТАЛЯХ
Формула Эйлера — Маклорена может произвести пугающее впечатление. Обычно она записывается так:
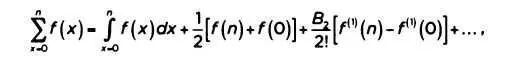
где В k— числа Бернулли, a f (x)— производные от f. Применение формулы состоит в том, что из правой части можно получить значения даже медленно сходящихся рядов. Эйлер использовал этот трюк в решении Базельской задачи, как мы увидим ниже.
СУММА, КОТОРАЯ СУММИРУЕТ НЕСУММИРУЕМОЕ
В 1735 году, во время своего первого российского периода, Эйлер сделал последнее из своих важных открытий в области анализа. Он вывел полезнейшую формулу, которая позволяет получать приблизительное значение интеграла, заменяя его на сумму, или приблизительное значение суммы, заменяя ее на интеграл. Независимо от Эйлера ее также открыл шотландский ученый Колин Маклорен. Так называемая формула Эйлера — Маклорена работает следующим образом: пусть дана функция f(x). Когда говорят о ее сумме, обычно имеют в виду две части, связанные между собой, но разные. Если использовать целые значения, то получится сумма
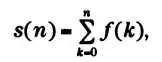
а когда ее складывают по всем х, получается интеграл:
i(n) = ∫ 0 nƒ(x)dx.
Кажется очевидным, что между s(n) и i(n) существует связь, но первая является дискретной суммой, а вторая — непрерывной. Формула Эйлера — Маклорена во многих случаях позволяет перейти от одной к другой. Если мы знаем s(n), то можем получить значение i(n), а если знаем i(n), можем высчитать s(n).
БАЗЕЛЬСКАЯ ЗАДАЧА: НАЧАЛО
По приезду в Петербург Эйлер получал 300 рублей, которых хватало на оплату проживания, дров для камина и масла для ламп. После того как он сменил Даниила Бернулли на посту профессора математики в 1733 году, Академия подняла его жалованье до 600 рублей. В том же году эта сумма еще увеличилась: Эйлер начал давать частные уроки и по предложению барона фон Мюнниха работать председателем экзаменационной комиссии в местной кадетской школе. Стабильное финансовое положение, сложившееся благодаря его новым обязанностям, позволило Эйлеру жениться на Катерине Гзель, дочери Георга Гзеля, художника швейцарского происхождения, работавшего в Академии искусств по особому приглашению Петра I. Церемония бракосочетания прошла 27 декабря 1733 года, после чего молодожены переселились в деревянный дом, "превосходно обставленный", по словам самого Эйлера, на Васильевском острове, недалеко от Академии наук. Через год у них родился первенец, Иоганн Альбрехт. Его крестным отцом стал фон Корф, бывший в то время президентом Академии. Этот факт свидетельствует о большом уважении, с которым относились к Эйлеру, что неудивительно, учитывая его огромный вклад в науку. Но это было еще не все. Буквально год спустя, в 1735-м, Эйлер поразил математическое сообщество гениальным озарением: он нашел решение Базельской задачи.
Читать дальше


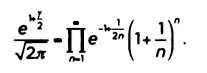
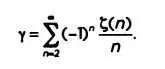
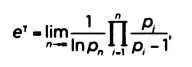
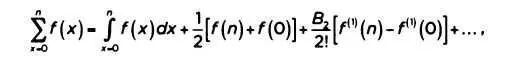
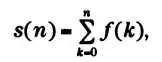





![Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-thumb.webp)



