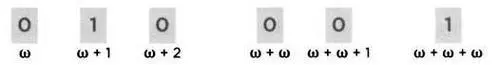Gustavo Pineiro - Бесчисленное поддается подсчету. Кантор. Бесконечность в математике.

Итак, у нас есть 2 1последовательности из одной цифры, 2 2последовательности из двух цифр, 2 3последовательности из трех цифр и так далее. Логично было бы предположить, что мощность последовательностей из «X 0цифр» будет равна 2 X0. Действительно, в «Обоснованиях» Кантор дает определение возведению мощностей в степень и основывает его на понятии, которое он назвал покрытием. Когда мы составляем бесконечную последовательность из нуля и единицы, утверждает Кантор, мы покрываем каждый элемент N нулем или единицей.

Ответить на вопрос, какова мощность множества всех бесконечных последовательностей, состоящих из 0 и 1, — значит покрыть N, используя два этих элемента. Всего способов «покрытия» чисел 0, 1 и 2 с использованием двух элементов — 2 3; покрытия чисел 0, 1, 2 и 3 — 2 4, значит, как писал Кантор, по определению, мощность всех способов покрытия N двумя элементами равна 2 X0 . К тому же, поскольку множество всех последовательностей нуля и единицы эквивалентно R, мы можем заключить, что и мощность R равна 2 X0 . Поэтому континуум-гипотезу можно сформулировать и как вопрос «равно ли 2 X0 X 1?».

Если бы мы покрывали N тремя элементами, то получили бы мощность 3 X0; другими словами, множество всех бесконечных последовательностей 0, 1 и 2 имеет мощность 3 X0. Но не стоит путаться. Сперва можно подумать, что 3 X0 больше 2 X0 , однако это не так. На самом деле 2 X0 = 3 X0. Чтобы доказать это, достаточно увидеть, что множество последовательностей нуля и единицы эквивалентно множеству последовательностей 0,1 и 2. За этим доказательством стоит идея, что поскольку последовательности нуля и единицы могут рассматриваться как числа, записанные в двоичной системе, таким же образом и последовательности 0, 1 и 2 могут быть представлены как числа, записанные в троичной системе. Таким образом, соответствие между двумя множествами устанавливается посредством изменения системы исчисления.

Исходя из определения степени мощностей, мы можем сказать, что, поскольку мощность ординальных чисел второго класса равна X 1 ?для этих ординальных чисел существует 2 X 1возможных покрытий; также, хотя и кажется очевидным, что 2 X 1больше 2 X0 , это еще не было доказано. Подчеркнем, что данное утверждение действительно нуждается в доказательстве. Мы не можем просто сказать, что поскольку X 1больше X 0, то и 2 X 1обязательно больше 2 X0 , — мы ведь уже видели, что хотя 3 и больше 2, при этом X 13 не больше 2 X0 . Отсюда следует: когда речь идет о бесконечности, то, что кажется само собой разумеющимся, не всегда верно. Как мы можем представить покрытие ординальных чисел второго класса? Заметим, что если дано количество X 1ординальных чисел второго класса, то каждое из его покрытий будет иметь X 1цифр, то есть по цифре на ординал.

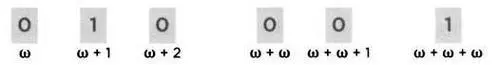
У покрытий ординалов второго класса более сложная структура, чем у N. Чтобы определить покрытие N, достаточно просто сказать, что оно «начинается с 01 и продолжается, повторяя эти цифры». Эта фраза полностью описывает покрытие 010101..., поскольку, пользуясь этим единственным правилом, мы знаем, какой цифрой — 0 или 1 — покрывать каждое натуральное число.

Но этого определения недостаточно для полного описания покрытия ординальных чисел второго класса, так как они устроены сложнее, чем натуральные числа. Ординалы второго класса начинаются с ω, ω + 1, ω + 2, ..., после бесконечного числа этапов переходят κω + ω,ω + ω+ 1,ω + ω + 2,..., после бесконечных переходов — к ω + ω + ω... и после бесконечного числа бесконечных переходов — κω + ω + ω + ω... (ω, взятому бесконечное число раз), ω + ω + ω + ω... (ω, взятое бесконечное число раз) + 1... и так далее.

Таким образом, если мы говорим, что покрытие ординалов второго класса «начинается с 01 и состоит из повторения этих цифр», это подскажет нам, какова будет только первая часть последовательности ω, ω + 1, ω + 2,... Перейдя κω + ω, мы должны указать способ начать покрытие заново. Оно может быть снова 01 или каким-то другим. И опять, когда мы дойдем до ω + ω + ω, мы должны будем начать все сначала; потом все сначала, дойдя до ω + ω + ω + ω, и так далее.

Если мы решим начинать каждый раз с 01, то у нас получится «базовое» покрытие N 010101..., которое будет повторяться несчетное количество раз.

Континуум-гипотеза гласит, что 2 X 0= X 1. Кантор не смог ни доказать, ни опровергнуть это утверждение. Обобщенная континуум-гипотеза была сформулирована Кантором в его «Обоснованиях» и расширяет предыдущую. По ней, не только 2 X 0= X 1но и 2 X 1= X 2, 2 X 2= X 3, 2 X 3= X 4и так далее. При жизни ученый так и не узнал, верные эти гипотезы или ложные.