Gustavo Pineiro - Бесчисленное поддается подсчету. Кантор. Бесконечность в математике.

Рассмотрим последний пример. Мы уже отметили, что у множества ординальных чисел первого класса (то есть натуральных) мощность равна X 0и что если мы прибавим к ним множество ординальных чисел второго класса (которое начинается c ω. ω + 1, ω + 2,...), то образованное множество будет иметь мощность X 1. Кантор же доказал, что и множество ординалов второго класса само по себе имеет мощность X 1. Если к множеству мощностью X 1(то есть только ординалов второго класса) прибавить множество мощностью X 0(ординалы первого класса), мы получим множество с мощностью X 1(ординалы первого и второго классов вместе); в терминах трансфинитной арифметики это означает, что X 0+ X 1= X 1(см. рисунок 4).

В действительности мы можем доказать, что дважды сложив одно и то же бесконечное кардинальное число, в результате получим его же (как в случае с X 0+ X 0= X 0), и если мы сложим два разных бесконечных кардинальных числа, то результатом будет большее из них ( X 0+ X 1= X 1). Следовательно, можно утверждать, что X 1+ X 1= X 1и X 2+ X 2= X 2.

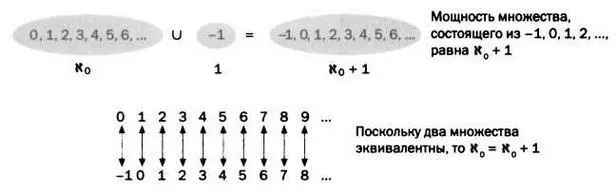
РИС. 3

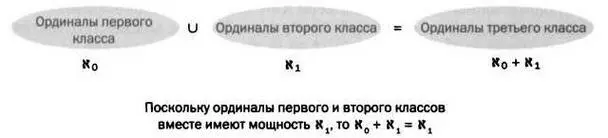
РИС. 4

Рассмотрим еще одну операцию трансфинитной математики, но сначала необходимо ввести несколько терминов. Множество надо понимать как вещь в себе, отличную от членов, которые его составляют. Так, Q, множество всех рациональных чисел, и I, множество иррациональных, являются каждое одним объектом. Тогда мы можем представить множество, составленное только этими двумя объектами — Q и I, — которое мы условимся называть D. Членов D всего два: это Q и I, следовательно, его мощность равна 2. Не следует путать D с объединением Q и I, которое получается, если в одно множество собрать все члены двух множеств, и в результате дает множество всех вещественных чисел R. Число 3/2, например, является членом Q и R, но не D. Здесь можно провести аналогию со множеством, образованным планетами солнечной системы, назовем его 5. В нем восемь членов: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун. С другой стороны, Земля сама по себе может быть представлена как множество, члены которого — человеческие существа.

В рамках трансфинитной арифметики помимо суммы мы можем определить произведение кардинальных чисел. Для этого надо обратиться к так называемому декартову произведению множеств. Если А и В — произвольные множества, их декартово произведение будет записываться как А x В и определяться как множество, образованное всеми парами, первые члены которых являются элементами А, а вторые — В. Как это делается в текстах по теории множеств, пара, образованная, например, числами 1 и 2, обозначается как (1,2). Порядок записи элементов очень важен, поскольку (1,2) — не та же самая пара, что (2,1). Поэтому обычно говорят об упорядоченных парах. Итак, если А — это множество, образованное числами 0 и 1, а В — числами 2,3 и 4, то А х В — это множество, состоящее из пар (0,2), (0,3), (0,4), (1,2), (1,3), (1,4). Обратим внимание на то, что А имеет мощность 2; В — мощность 3, а А х В — мощность 6. Как следствие из предыдущего примера, произведение мощности А на мощность В будет мощностью А x В (в отличие от того, что происходит в случае сложения, здесь не имеет значения, есть ли у А и В общие члены). Чему равно X 0х X 0? Если мы возьмем множество всех натуральных чисел N (мощность которого, как мы знаем, равна X 0), то исходя из предыдущего определения X 0∙ X 0— мощность N x N (множество всех пар натуральных чисел). Далее будет доказано, что N х N счетное.

Чтобы доказать, что N х N счетное, запишем все составляющие его пары в последовательность. Начнем с единственной пары, дающей в сумме 0, потом пары, сумма которых равна 1, затем — 2 и так далее.

(0,0), (0,1), (1,0), (0,2), (1,1), (2,0), (0,3), (1,2), (2,1), (3,0),...

Эта запись позволяет нам установить взаимно однозначное соответствие между «индивидуальными» натуральными числами и парами натуральных чисел:

Это соответствие доказывает, что N х N счетное, следовательно, его мощность равна X. Итак, с одной стороны, произведение мощностей дает понять, что мощность N x N равна X 0∙ X 0. С другой стороны, мы только что доказали: мощность N х N равна X 0. Отсюда следует, что X 0∙ X 0= X 0.