Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

π — Пи

ЗА ПРЕДЕЛАМИ БЕСКОНЕЧНОСТИ

Прошло четыре тысячи лет, а эта тайна

все еще остается тайной.

И хотя каждый школьник изучает π,

этот знакомый символ

по-прежнему скрывает в себе бездны

величайшей сложности.

Почему мы выбрали π как вечный символ

мужского начала?

Все дело в знаках и указателях.

Если π — это история

долгой борьбы за достижение недостижимого,

то это и портрет

легендарного покорителя неизведанного,

идущего вперед в поисках Знания.

Пи говорит нам о мужчинах, обо всех мужчинах,

об их научном гении,

об их тяге к приключению, об их готовности

к действию

и об их стремлении к недостижимому.

Самые ранние приближения числа π дошли до нас от древних вавилонян, использовавших значение 3 1/ 8, и от египтян, которые пользовались значением 4( 8/ 9) 2, что в десятичных дробях выражается, соответственно, как 3,125 и 3,160.

Позднее, в Древней Греции, первым в череде гениев с необычайной страстью к числу π был Архимед — мыслитель, предпочитавший иметь дело с миром реальности, в отличие от Евклида, существовавшего в мире абстракций. Среди многочисленных изобретений Архимеда были гигантская катапульта и система зеркал, с помощью которых он сфокусировал солнечные лучи так, что поджег римские корабли во время осады Сиракуз. А кроме того, он оказался первым, кто предложил метод вычисления числа π.

Итак, Архимед нарисовал окружность, а затем построил два шестиугольника: один — вписанный в окружность, а другой — описанный вокруг нее, как указано на рисунке.

Одно это уже говорит нам, что значение числа π должно лежать где-то между 3 и 3,46 — это можно определить, вычисляя периметры двух шестиугольников. Если принять диаметр окружности равным 1, то периметр внутреннего шестиугольника равен 3, что меньше, чем длина окружности, равная π , что в свою очередь меньше, чем периметр внешнего шестиугольника, равный 3√2, то есть с точностью до двух десятичных разрядов — 3,46. (Архимед находил периметр внешнего шестиугольника, используя метод, который по сути был довольно канительным предшественником тригонометрии и который слишком сложен для того, чтобы здесь его приводить.) Итак,

3 < π < 3,46.

Если теперь повторить вычисление, используя два правильных многоугольника с более чем шестью сторонами, то для π получится более узкий интервал. Дело в том, что чем больше у многоугольника сторон, тем ближе его периметр к длине окружности, в чем можно убедиться, глядя на приведенный выше рисунок с двенадцатиугольником. Многоугольники ведут себя подобно стенам, смыкающимися вокруг π , зажимая его снаружи и изнутри, между все более узких пределов. Архимед начал с шестиугольников, а в конце довел дело до многоугольников с 96 сторонами, что позволило ему вычислить π следующим образом:

3 10/ 71< π < 3 1/ 7.

Это дает 3,14084 < π < 3,14289 — точность в два десятичных разряда.

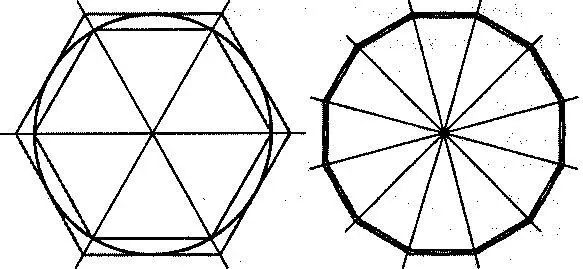
Шестиугольники Двенадцатиугольники

Однако охотники за числом π не собирались на этом останавливаться. Все, что требовалось, дабы подобраться поближе к истинному значению этого числа, — это строить многоугольники со все большим числом сторон. Лю Хуэй, живший в Китае в III веке, применил сходный метод, используя площадь многоугольника с 3072 сторонами, и получил пять десятичных разрядов числа π : 3,14159. Два столетия спустя Цзу Чунчжи и его сын Цзу Гэнчжи продвинулись дальше еще на одну цифру, до 3,141592, что потребовало многоугольника с 12 288 сторонами.

Грекам и китайцам мешали неуклюжие обозначения. Когда в конце концов математики стали применять арабские числительные с десятичной запятой, прежние рекорды тут же пали. В 1596 году голландский учитель фехтования Лудольф ван Цейлен, используя метод удвоения, дошел до многоугольника с 60 × 2 29сторонами и нашел значение π с точностью до 20 десятичных знаков. Опус, в котором он напечатал свой результат, заканчивался так: «У кого есть охота, пусть подойдет ближе». Он продолжал вычислять и получил число π с точностью до 32 и затем 35 десятичных знаков, каковые и были высечены на его надгробии. В Германии die Ludolphsche Zahl — число Лудольфа, или лудольфово число, — до сих пор допустимо в качестве названия числа π.