Чарльз Сейфе - Ноль - биография опасной идеи

Несмотря на тяжелое детство [27] Когда Ньютону было три года, его мать снова вышла замуж и переехала. Родив второму мужу троих детей, она практически не уделяла внимания Исааку. Даже после смерти отчима Исаак и его мать мало общались, хотя, получив после смерти мужа хозяйство, мать пыталась переложить на плечи юного Ньютона управление фермой (прим. авт.). и желание матери, чтобы он стал фермером, Ньютон поступил в 1660 году в Кембриджский университет и преуспел. За несколько лет он создал систематический метод разрешения проблемы касательной: теперь он мог вычислить касательную к любой плавной кривой в любой точке. Этот процесс представляет собой первую часть математического анализа, теперь известную как дифференциальное исчисление. Впрочем, способ Ньютона не особенно похож на тот, которым мы пользуемся сегодня.

Стиль дифференцирования Ньютона основывался на флюксиях (производных) — потоках — математических выражений, которые он называл флюентами (переменными). Как пример флюксий Ньютона рассмотрим уравнение y = x 2+ x + 1. В этом уравнении флюентами являются x и y; Ньютон полагал, что x и y меняются — текут — с течением времени. Скорость их изменения — их флюксии — он обозначал как x́ и ý соответственно.

Метод дифференцирования Ньютона основывался на одном приеме: он позволял флюксиям изменяться, но изменяться бесконечно мало. По сути, он не давал им времени течь. В обозначениях Ньютона y в этот момент менялся на (y + оý), в то время как x менялся на (x + оx́). (Буква «о» представляла собой количество прошедшего времени; оно было почти нолем, но не совсем, как мы увидим.)

Уравнение тогда принимает вид:

(y + оý) = (x + оx́) 2+ (x + оx́) + 1.

Раскрытие выражения (x + оx́) 2 дает нам y + оý = x 2+ 2x(оx́) + (оx́) 2+ x + оx́ + 1. Приведение членов дает y + оý = (x 2+ x + 1) + 2x(оx́) + 1(о x́ ) + (о x́ ) 2. Поскольку y = x 2+ x + 1, мы можем вычесть y из левой части уравнения и x 2+ x + 1 из правой. Это дает нам оý = 2x(оx́) + 1(оx́) + (оx́) 2. Дальше следует жульнический прием. Ньютон заявил, что поскольку оx́ на самом деле очень, очень мал, о x́́ 2еще меньше и исчезает. По сути это был ноль, и его можно было игнорировать. Это дает нам оý = 2x(оx́) + 1(оx́), а это значит, что оý / оx́ = 2x + 1. Это и есть угол наклона касательной в любой точке кривой (рис. 26).

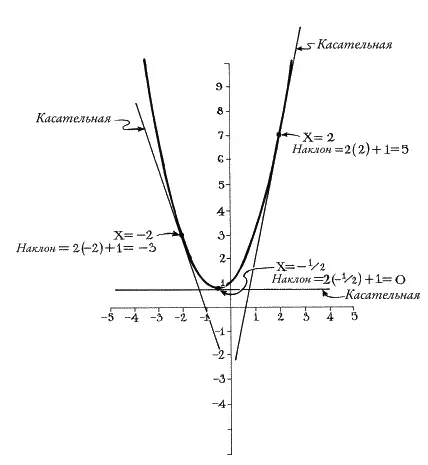
Рис. 26.Чтобы найти угол наклона в любой точке параболы y = x 2+ x + 1, нужно использовать формулу 2x + 1

Бесконечно малый период времени о выпадает из уравнения, оý / оx́ превращается в ý / x́, и об о больше не нужно думать.

Метод давал правильный ответ, но ньютоновское действие исчезновения очень смущало. Если, как настаивал Ньютон, (оx́) 2, (оx́) 3и более высокие степени оx были равны нолю, то и само оx́ должно быть равно нолю [28] Если вы перемножаете два числа и получаете ноль, то одно из них должно быть равно нолю. (В математических терминах: если ab = 0, то или a = 0, или b = 0.) Это значит, что если a 2 = 0, то aa = 0 и тем самым a = 0. . С другой стороны, если оx́ — ноль, то деление на оx́, как мы делали в конце, то же самое, что деление на ноль — как и самый последний шаг избавления от о в верхней и нижней части выражения оý / оx́. Деление на ноль запрещено математической логикой.

Ньютоновский метод флюксий был очень сомнителен. Он предполагал незаконную математическую операцию, однако обладал одним огромным преимуществом. Он работал. Метод флюксий не только разрешал проблему касательной, он разрешал и проблему площадей. Нахождение площади под кривой (или прямой, которая является одной из разновидностей кривой) — операция, которую мы теперь называем интегрированием, — всего лишь действие, обратное дифференцированию. Как дифференцирование выражения y = x 2+ x + 1 дает уравнение для наклона касательной y = 2 x + 1, интегрирование уравнения y = 2 x + 1 дает формулу для определения площади под кривой. Эта формула — y = x 2+ x + 1; площадь под кривой, ограниченной точками x = a и x = b просто равна (b 2+ b + 1) — ( a 2+ a + 1) ( рис. 27 ). (Технически формула имеет вид y = x 2+ x + c , где c есть любая константа. Процесс дифференцирования уничтожает часть информации, так что процесс интегрирования не дает вам точно тот ответ, который вы ищете, если только вы не добавите недостающие данные.)