Чарльз Сейфе - Ноль - биография опасной идеи

Имея в руках такой инструмент, Ньютон смог создать простое дифференциальное уравнение, описывающее движение всех тел во Вселенной: F = mx˝, где F — сила, действующая на тело, а m — его масса. (На самом деле это не вполне универсальный закон, поскольку уравнение верно, только когда масса объекта постоянна. Более общая версия закона Ньютона [29] Именно так закон формулировался Ньютоном, а более привычная нам формулировка (сила равна массе, умноженной на ускорение) была придумана для школьников, которые начинают изучать механику раньше анализа. выглядит так: F = ṕ, где p — количество движения, или импульс тела. Конечно, уравнения Ньютона были со временем усовершенствованы множеством ученых, в том числе Эйнштейном.)

Если у вас имеется уравнение, которое говорит вам о силе, приложенной к телу, дифференциальное уравнение точно сообщит вам, как тело движется. Например, мяч в свободном падении движется по параболе, в то время как пружина без трения вечно раскачивается туда и сюда, а под действием трения медленно останавливается (рис. 28). Какими бы разными ни казались эти исходы, все они описываются одним и тем же дифференциальным уравнением.

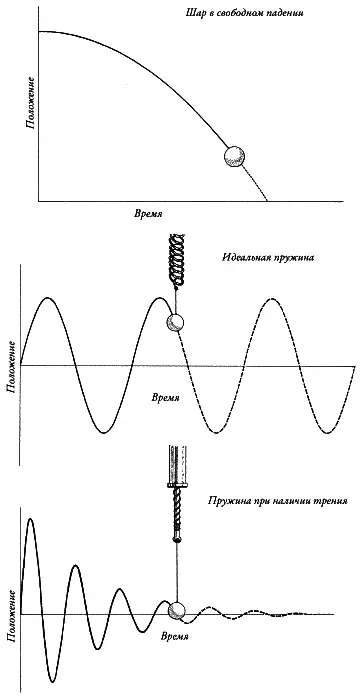
Рис. 28.Различные движения, описываемые одним и тем же дифференциальным уравнением

Точно так же, если вам известно, как движется тело — будь это мячик или гигантская планета, — дифференциальное уравнение скажет вам, какого рода сила к нему приложена. (Триумф Ньютона заключался в выведении уравнения, описывавшего силу притяжения и форму орбит планет. Раньше предполагалось, что сила была пропорциональна 1 / r 2, и когда из дифференциальных уравнений Ньютона были получены эллиптические орбиты, люди стали верить в правоту Ньютона.) Несмотря на возможности анализа, ключевая проблема сохранялась. Работы Ньютона основывались на очень шатком фундаменте — делении ноля на самого себя. Труды его соперника имели тот же недостаток.

В 1673 году почтенный немецкий юрист и философ посетил Лондон. Его имя было Готфрид Вильгельм Лейбниц. Они с Ньютоном едва не разорвали пополам научный мир, хотя ни один из них не мог разрешить проблему ноля, которой был пронизан математический анализ.

Никто не знает, не ознакомился ли во время визита в Англию тридцатитрехлетний Лейбниц с неопубликованной работой Ньютона. Однако между 1673 и 1676 годами, когда Лейбниц в следующий раз посетил Лондон, он тоже создал анализ, хотя и в несколько иной форме.

Глядя назад, можно заключить, что Лейбниц сформулировал свою версию независимо от Ньютона, хотя споры по этому поводу не прекращаются. Двое ученых в 1670-е годы вели переписку, так что очень трудно определить, как они влияли друг на друга. Впрочем, хотя две теории дают одинаковые ответы, условные обозначения — и философия — очень разнятся.

Ньютон не любил бесконечно малые величины, маленькие о в его флюксиях иногда вели себя как ноль, а иногда — как отличные от ноля числа. В определенном смысле эти бесконечно малые были бесконечно малы, меньше любого положительного числа, но все же каким-то образом больше ноля. Для математиков того времени это была смешная концепция.

Ньютона смущали бесконечно малые в его уравнениях, и он заметал их под ковер. Маленькие о в его уравнениях были всего лишь посредниками, костылями, которые чудесным образом исчезали к концу выкладок. С другой стороны, Лейбниц наслаждался бесконечно малыми. Там, где Ньютон писал о x́, Лейбниц писал dx — бесконечно малый кусочек x . Бесконечно малые выжили без изменений во всех расчетах Лейбница; действительно, производная от y по x было не свободным от бесконечно малых отношением флюксий ý / x́, а отношением бесконечно малых dy / dx.

В исчислении Лейбница с этими dy и dx можно было обращаться как с обычными числами, поэтому современные математики и физики обычно используют обозначения Лейбница, а не Ньютона. Дифференциальное исчисление Лейбница обладало той же силой, что и метод Ньютона, а благодаря обозначениям даже несколько большей. Тем не менее под всеми математическими ухищрениями дифференциалы Лейбница имели ту же запретную природу 0 / 0, которая вредила флюксиям Ньютона. До тех пор, пока сохранялся этот недостаток, исчисление продолжало основываться скорее на вере, чем на логике. (На самом деле вера очень сильно влияла на Лейбница, когда он создавал новые математические методы, например двоичную систему счисления. Любое число могло быть записано как ряд нолей и единиц. Для Лейбница это было созданием ex nihilo, созданием Вселенной из ничего, большего, чем Бог / 1 и пустоты / 0. Лейбниц даже пытался убедить иезуитов использовать это знание для обращения китайцев в христианство.)