Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

«Впрочем, — подумал студент, — даже одна моя бабушка — это настоящее маленькое солнышко. От нее в доме всем теплее и светлее на душе».

Очевидно, длительность свечения угольного или нефтяного Солнца составит t = QM ⊙/ L ⊙, где M ⊙= 2 · 10 30кг и L ⊙= 4 · 10 26Вт — масса и светимость Солнца; Q = 2 · 10 7Дж/кг. Тогда t = 3000 лет. Это даже короче письменной истории человечества.

У этой задачи интересная история. Еще в середине XIX века астрономы поняли, что тепло, выделяющееся при химических реакциях, не может поддерживать солнечную светимость на современном уровне дольше нескольких тысяч лет (см. задачу «Солнце из угля»). Тогда немецкий врач Юлиус Майер (1814–1878), исследования которого привели к открытию закона сохранения энергии, предположил, что Солнце светит за счет тепла, выделяющегося при падении на его поверхность комет и метеоритов. Но притяжение Солнца не может разогнать падающие тела до скорости свыше 618 км/с (вторая космическая скорость на поверхности Солнца). Учитывая, что при торможении в тепло переходит кинетическая энергия тела ( mv 2/2), легко подсчитать, что для поддержания светимости Солнца на него ежегодно должна падать масса, почти равная массе Луны. При таком темпе аккреции через 30 млн лет масса Солнца возросла бы вдвое по сравнению с нынешней. Как выяснилось позже, именно падение околозвездного вещества обеспечивает высокую светимость самых молодых звезд и некоторых старых «звездных остатков» — белых карликов, нейтронных звезд, черных дыр. Но к Солнцу и подобным ему звездам среднего возраста, пребывающим «в полном расцвете сил», процесс аккреции отношения не имеет. Астрономы XIX в. подтвердили, что не наблюдают падения комет на Солнце в таком количестве.

Обдумывая идею Майера, немецкий естествоиспытатель Герман Гельмгольц (Hermann von Helmholtz, 1821–1894) предположил, что на Солнце не обязательно должно что-то падать снаружи: «падать» на него может… вещество самого Солнца. Посмотрим еще раз на формулу для кинетической энергии ( mv 2/2): большой приток энергии обеспечивается либо высокой скоростью, либо большой массой. Поддержание высокой температуры звезды может происходить вследствие ее медленного сжатия. Сила тяготения при сжатии звезды совершает над газом работу, и это приводит к его нагреву. По расчетам английского физика Уильяма Томсона, барона Кельвина (William Thomson, 1st Baron Kelvin, 1824–1907), чтобы поддерживать свою светимость на современном уровне, Солнце должно ежегодно сжиматься всего на 90 метров, т. е. примерно на 1/15 000 000 долю своего радиуса. По оценке Томсона, сжимающееся Солнце могло светить не менее ярко, чем сегодня, на протяжении почти 30 млн лет.

Проверим это самостоятельным расчетом. Если ускорение силы свободного падения g = GM/R 2, то работа силы тяжести по перемещению массы m на расстояние h составляет

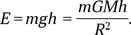
Если сжатие звезды происходит под действием собственной силы тяжести, то m = M и h ≈ R . Тогда

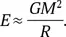
Это приблизительная оценка, но если вы умеете интегрировать, то можно доказать это точно. Гравитационная энергия тела, выделяющаяся при его сжатии от очень большого размера до радиуса R , составляет α GM 2 /R , где α — коэффициент порядка единицы, зависящий от распределения массы внутри тела.

Если сжатие происходит медленно, квазистатически, то в недрах звезды должно поддерживаться гидростатическое равновесие, а значит, по мере сжатия должны возрастать давление и температура. Несложно показать, что выделяющаяся при сжатии гравитационная энергия будет при этом делиться пополам: одна половина пойдет на нагрев недр звезды, а вторая — на излучение. Для знатоков теоретической механики сошлюсь на теорему о вириале. А для любителей небесной механики и космонавтики — на соотношение энергий у тел, движущихся с первой и второй космическими скоростями.

Приняв α = 1 (к большой ошибке это не приведет), получим характерное время излучения сжимающейся звезды t ≈ GM 2/(2 RL ), где L — светимость (т. е. мощность излучения) звезды. В честь Кельвина и Гельмгольца астрофизики называют эту величину временем Кельвина — Гельмгольца ( t KH). Для Солнца t KH ≈ GM 2 ⊙ /(2R ⊙ L ⊙ ) , где L ⊙ = 4 · 10 26Вт, M ⊙= 2 · 10 30кг и R ⊙= 7 · 10 8м — светимость, масса и радиус Солнца. Подставляя эти значения в формулу, получим t KH= 30 млн лет — в точности как у Кельвина! Это характерное время высвечивания Солнцем его гравитационной энергии связи.