Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

Такие явления называют покрытиями звезд Луной. Максимальной длительности они достигают при центральных покрытиях, когда, с точки зрения наблюдателя, путь светила проходит через центр лунного диска. Скорость перемещения Луны на фоне звездного неба задана длительностью сидерического лунного месяца (27,32 сут). Отсюда средняя угловая скорость Луны на звездном небе равна 360°/27,32 = 13,18°/сут, или 0,55° в час. Поскольку угловой диаметр лунного диска равен примерно 0,5°, звезда скроется за ним не более чем на час. А если покрытие не центральное, то на любое время короче часа.

В конце первой декады ноября весьма велико уравнение времени, оно превосходит 15 минут (см. в «Справочнике любителя астрономии», 2002, рис. 171 на с. 246, или в книге «Вселенная от А до Я», 2012, статью «Уравнение времени»). Поэтому истинная местная солнечная полночь в Москве 9/10 ноября наступила раньше, в 0 ч 15 мин московского декретного времени. Первое наблюдение отстояло от нее менее чем на 6 ч 45 мин, а второе — более чем на 7 ч 15 мин. (Автор идеи этой задачи — Н. Н. Самусь.)

Самолет должен лететь на запад со скоростью вращения Земли: V = 40 000 км / 24 часа = 463 м/с. Эта скорость (1,5 скорости звука) вполне доступна для некоторых современных самолетов.

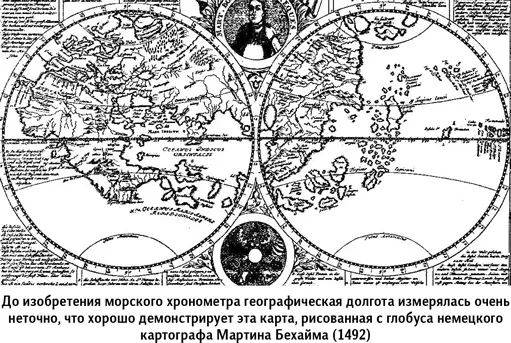
Имея секстант — а у моряков он в той или иной форме был всегда, — можно весьма точно измерить географическую широту места наблюдения, например, по высоте Полярной звезды. А вот с долготой дело обстоит значительно хуже. До появления надежных часов, так называемого морского хронометра, определение долготы было очень неточным. Ведь долгота — это угол между Гринвичским меридианом и меридианом наблюдателя. Его измеряют, фиксируя прохождение определенных звезд через небесный меридиан. Если у штурмана есть на борту точные часы, идущие по времени Гринвича, и астрономические таблицы, в которых указано, когда в Гринвиче та или иная звезда проходит через гринвичский меридиан ( t 0), то штурману остается лишь заметить момент прохождения этой звезды через местный меридиан ( t 1) и определить разницу моментов прохождения — наблюденного и указанного в таблице для Гринвича (∆ t = t 0− t 1). Это и есть долгота (λ) в виде часов, минут и секунд. Из часовой меры ее легко перевести в градусную: λ = 360° · ∆t/24 часа. Разумеется, здесь 24 часа звездного времени, поскольку это длительность одного оборота Земли вокруг оси.

Разумеется, есть и более точные методы определения долготы и широты, чем фиксация моментов пересечения меридиана (он ведь не нарисован на небе!). Например, метод Сомнера, состоящий в измерении зенитного расстояния звезд («Небо и телескоп», 2017, раздел 1.5.1). Но все без исключения подобные методы требуют точной фиксации времени измерения, т. е. наличия на корабле точных часов. В настоящее время определение моментов не представляет трудностей — часы всегда можно проверить по радио. До появления радио морякам приходилось возить с собой часы, специально приспособленные для хранения времени на корабле — морской хронометр, изобретенный английским мастером Гаррисоном в XVII в. До изобретения хронометра время определяли по положению Луны среди звезд или по конфигурации спутников Юпитера. Их заранее рассчитывали астрономы и публиковали в виде таблиц для штурманов. А пока все это не появилось, «лот, широта и осмотрительность» были главными помощниками штурмана и капитана.

На Земле солнечные часы остановиться не могут: солнце непрерывно перемещается по небосводу, а значит, и тень от гномона тоже перемещается по циферблату часов. Правда, можно вообразить ситуацию, когда солнечные часы «практически» остановятся. Например, горизонтальные солнечные часы на экваторе в дни весеннего и осеннего равноденствий. В эти дни солнце движется практически по экватору. Поэтому тень от вертикального гномона не будет менять свой азимут, а лишь будет укорачиваться и удлиняться. А в местный солнечный полдень она вообще исчезнет!

Другая ситуация — это солнечные часы на планете, обращающейся вокруг своей звезды по круговой орбите и синхронно вращающейся вокруг своей оси. Среди экзопланет таких немало, но в Солнечной системе подобных нет. У нас много синхронно вращающихся тел среди спутников планет, но ни одна планета синхронно не обращается вокруг Солнца. Ближе всех к этому состоянию Меркурий, у которого суточное вращение находится в резонансе 3:2 с орбитальным обращением: за время трех оборотов вокруг оси он совершает два оборота вокруг Солнца. Но вот что любопытно: Меркурий движется по заметно вытянутой орбите, поэтому в области перигелия угловая скорость его орбитального движения возрастает и сравнивается с угловой скоростью суточного вращения. В эти периоды Солнце на небосводе Меркурия действительно останавливается! Замирает и тень на циферблате солнечных часов.