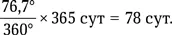Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

1) Орбита Венеры наклонена к эклиптике на 3,4°, а угловой размер солнечного диска, наблюдаемого с Земли, 0,5°, поэтому мы можем увидеть Венеру на фоне Солнца только в те моменты, когда она и Земля находятся вблизи одного из узлов орбиты Венеры. Долгота ее восходящего узла 76,7°. Чтобы Земле от точки весеннего равноденствия (21 марта) пройти такой путь по своей орбите (считаем ее круговой), требуется

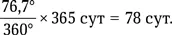
Получаем дату возможного прохождения Венеры по Солнцу в районе восходящего узла:

21 марта + 78 сут = 7 июня.

Конечно, дата приблизительная, поскольку календарь конкретного года (либо простого, либо високосного) может менять ее на 1–2 дня. К тому же угловой размер Солнца делает возможным прохождение по его диску в пределах 2–3 дней до или после пересечения Венерой эклиптики (0,5°/sin 3,4° = 8,4°; их Венера проходит за 5 суток). Ну а вторая возможная дата прохождения наступает, когда Земля проходит у нисходящего узла венерианской орбиты — полгода спустя.

2) Через окрестности узла орбиты Венеры должны одновременно пройти Земля и Венера с точностью до 2–3 сут, т. е. до 1/ 100года. Орбитальный период Венеры — 0,61521 года. Умножая его последовательно на целые числа (1, 2, 3, …), впервые получим целое число с точностью выше 1/ 100при умножении на 13:

0,61521 года × 13 = 7,998 года.

То есть через 13 оборотов Венеры и 8 оборотов Земли они снова сходятся у того же узла орбиты Венеры.

3) В этом случае нам надо решить уравнение:

0,61521 года × ( k + 0,5) = ( n + 0,5) года,

где k и n — целые числа, с точностью до 1/ 100.

Приводим уравнение к виду

0,61521 k — 0,192395 = n

и методом перебора находим пары ( k = 171, n = 105) и ( k = 197, n = 121).

Начальник станции был вежливый человек. Он согласился с замечанием и пообещал исправить оплошность. «Однако, — добавил он, — поскольку станция находится на свободно дрейфующей льдине, которую течением и ветром сносит иногда на несколько километров в сутки, отметку земной оси придется каждый день переставлять. Для этого понадобится дополнительная штатная единица, а также снегоход или вертолет и топливо». Руководитель комиссии замахал руками и сказал, что в смету эти расходы не заложены, дополнительных фондов нет и он не выделит на это ни копейки. Начальник станции пожалел, что такая хорошая идея не может быть реализована. «Бюджет — святое дело», — вздохнул он, и дискуссия о земной оси завершилась к обоюдному удовольствию. Мораль: учитесь разговаривать с чиновниками!

Как известно, звездные сутки длятся 23 часа 56 минут. Следовательно, в следующий раз звезда взойдет в 23:57 того же дня. Но между двумя восходами звезда должна пересечь линию горизонта при заходе. Следовательно, в течение текущих суток звезда появится на горизонте еще как минимум дважды.

Но и это не предел! Звезда может проходить видимую (из данного места) часть своего пути очень низко над горизонтом, и тогда после второго восхода она еще может успеть сесть за оставшиеся до окончания суток три минуты. Поэтому полный ответ: звезда пересечет горизонт еще минимум 2, но, возможно, и 3 раза.

Задача кажется очень легкой: искомая точка — Северный полюс. Но не торопитесь: существуют и другие решения.

Кроме одной точки на Северном полюсе существует также бесконечное множество точек в окрестности Южного полюса, также удовлетворяющих условию задачи. Они лежат на концентрических окружностях с центром в Южном полюсе, имеющих радиусы Rk = 100 × (1 + 1/ 2π k ) км, где k = 1, 2, 3, … Например, при k = 1 мы выходим с расстояния около 116 км от полюса и, двигаясь на юг, приближаемся к нему до расстояния 16 км. Затем поворачиваем на восток и обходим вокруг полюса целый круг (длина окружности 2π · 16 = 100 км. Затем по уже пройденному пути возвращаемся на север в исходную точку. При k = 2 придется сделать два обхода вокруг полюса по кругу вдвое меньшего размера. При этом движение происходит все время строго на восток. Между расстояниями 116 и 100 км от Южного полюса заключено бесконечное число окружностей, все точки которых удовлетворяют условию задачи.

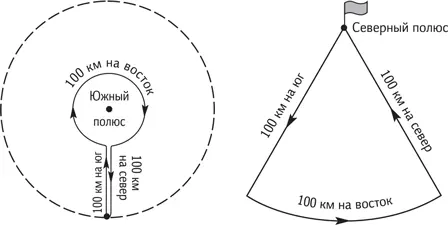
Решая эту задачу, мы считали поверхность Земли в районе полюса плоской, поскольку расстояния невелики. Но можно было бы учесть кривизну Земли. Это имело бы смысл, если бы в условии задачи был задан путь не 100 км, а 1000 км, 10 000 км, 20 000 км. Попробуйте решить эту задачу с такими условиями. Последнее из них особенно интересно. Землю мы считаем шаром с окружностью 40 000 км по экватору.