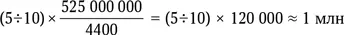Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

2) Разобравшись с природой пепельного света Луны, мы легко ответим на второй вопрос: поскольку с обратной стороны Луны Земля не видна, то и пепельного света там нет.

3) Поверхностная яркость пепельного света невелика и не всегда способна соперничать с яркостью голубого неба. Чем темнее сумеречное небо, тем легче заметить пепельный свет. Весной Солнце находится близ точки весеннего равноденствия, поэтому после его захода на западе эклиптика круто поднимается над горизонтом, и молодая Луна, которая всегда недалеко от эклиптики, стоит высоко, на фоне заметно потемневшего сумеречного сегмента неба. Такая же ситуация и осенью на востоке.

Чтобы получить аккуратную оценку, необходимо сделать некоторые предположения о «наблюдательности наблюдателя». Мой личный опыт подсказывает, что при длительном наблюдении ночного неба поле зрения человека ограничено окружностью диаметром 50÷60°. Значит, в атмосфере, на высоте 90 км, мы охватываем зрением круг радиусом около 90 км × tg (55°/2) = 37 км. Площадь этого круга около 4400 км 2. А полная площадь атмосферы на этой высоте равна 4π ( R ⊕+ 90 км) 2, где R ⊕= 6371 км — средний радиус Земли. Вычислим эту площадь «метеорной сферы» и получим около 525 млн км 2. Следовательно, в атмосфере Земли вспыхивает

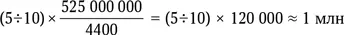
метеоров за час. Это около 24 млн метеоров в сутки. Или около 300 метеоров в секунду.

Масса метеороидов, вызывающих вспышки метеоров, обычно оценивается в 0,01 г. Проверить порядок этой величины мы с вами можем. Используем связь между болометрической звездной величиной ( m b) и потоком энергии вблизи наблюдателя (Сурдин, 2012; статья «Звездная величина»):

f = 2,5 ×10 –8× dex{–0,4 m b} Вт/м 2

Обозначение «dex{…}» означает «десять в степени…». Используя эту формулу для визуального диапазона, перейдем к видимым звездным величинам:

f = 2,5 · 10 –8× 10 — 0,4 mВт/м 2.

Пусть m = 3, расстояние до метеора 100 км, а продолжительность его вспышки составляет 1 сек. Тогда f = 1,6 · 0 –9Вт/м 2, полная мощность вспышки F = 4π f (100 км) 2= 200 Вт, а ее полная энергия E = 200 Дж. Весьма произвольно примем эффективность преобразования кинетической энергии метеороида ( MV 2/2) в свет равной η = 10 %. При средней скорости метеороида 30 км/с это даст его массу

что практически не отличается от 0,01 г.

Профессиональные исследователи метеоров дают весьма близкие оценки: «При условии, что метеор достигает 1 звездной величины при скорости вхождения в атмосферу Земли 40 км/с, загорается на высоте 100 км, а потухает на высоте 80 км, при длине пути в 60 км и расстоянии до наблюдателя в 150 км, продолжительность полета составит 1,5 сек, а средний размер составит 0,6 мм при массе 6 мг» (Петров В. Н. Некоторые проблемы физики метеоров // УФН. 1939. Т. 22, вып. 4. С. 449).

Итак, мы выяснили, что принимаемая обычно масса частицы, вызывающей вспышку метеора, действительно порядка 0,01 г. Это масса пляжной песчинки. Умножив эту массу на количество наблюдаемых в сутки метеоров (24 млн), получим 240 кг/сут. В год это около 100 т. Весьма мало по сравнению с массой самой Земли.

Разумеется, кроме тех частиц, что регулярно вызывают вспышки метеоров, еще бывают кратковременные, но обильные метеорные дожди, изредка падают крупные метеориты и невидимыми остаются многочисленные очень мелкие частицы. Например, если раз в столетие падает метеорит размером 20 м (Тунгусский, Челябинский), то в среднем это дает еще 100 т/год.

Тут сразу две астрономические неточности. Во-первых, период между восходами Луны около 25 часов, поэтому бывают сутки без восходов Луны. Во-вторых, по этой же причине (25 часов длиннее солнечных суток) восходы Луны происходят в произвольное время суток, а не только по ночам.

Утверждение Б. Паркера неверно. На разных (по абсолютной величине) широтах одинаковое линейное смещение по-разному изменяет долготу, поскольку длина параллелей зависит от широты. Расположение городов, а значит, и расстояние между городами, лежащими на разных широтах, при этом изменится. Это легко понять на простом примере. Пусть два города лежат на одном меридиане. Передвинем их по долготе на одинаковое линейное расстояние. После этого они окажутся на разных меридианах, но на исходных широтах. Теперь расстояние между ними определяется длиной гипотенузы, хотя исходное расстояние было лишь катетом в этом треугольнике. А гипотенуза, как известно, длиннее катета.