Влияние несферичности гравитационного поля Земли на движение Апофиса до и после сближения 2029 г. исследовалось численным образом в работе [Giorgini et al., 2008]. При отсутствии тесных сближений с Землей влияние ее несферичности на движение астероида является минимальным. Однако прогноз сближения в 2036 г. при использовании сферической модели Земли дает ошибку порядка 19 000 км по сравнению с прогнозом, учитывающим ее сжатие. Прочие зональные гармоники вносят возмущения, по крайней мере, на три порядка меньшие. Долготная вариация гравитационного поля Земли приводит к уклонению порядка 100 км в 2036 г.
Влияние возмущений, вызываемых тепловым излучением астероида (эффект Ярковского), рассмотрено в разделе 7.7.6.
Обратимся теперь к проблеме численного интегрирования уравнений движения малых тел. Существует большое число методов численного интегрирования дифференциальных уравнений движения, способных обеспечить достаточно высокую точность прогноза движения опасного астероида на длительных интервалах времени (см., напр., [Бордовицына, 1984; Бордовицына, Авдюшев, 2007]). В различных организациях для этой цели используются методы Булирша — Штера, Эверхарта, Рунге — Кутты — Фельберга, Адамса и другие. В ЛРД НАСА на протяжении многих лет широко используется метод с переменным шагом Адамса — Крога для интегрирования дифференциальных уравнений второго порядка [Krogh, 1968; 1974]. Метод применяется при построении численных эфемерид больших планет и Луны при проведении многочисленных космических экспедиций к телам Солнечной системы. Он многократно доказал свою точность и эффективность. Метод реализован с двукратной точностью (ошибка порядка 10 -14на каждом шаге) и даже четырехкратной точностью (ошибка порядка 10 -19на одном шаге). Правда, четырехкратная точность требует примерно в 30 раз больше компьютерного времени.
В ИПА РАН при построении численных эфемерид больших планет и Луны, как и при расчетах эфемерид малых тел, широко используется метод численного интегрирования Эверхарта [Everhart, 1974a; 1974b], интегратор RADAU с двойной точностью. Метод позволяет, в частности, интегрировать уравнения вида 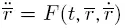 (зависимость правых частей от
(зависимость правых частей от 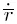 появляется при учете релятивистских членов и негравитационных эффектов). Метод дает возможность вести вычисления с различной точностью в зависимости от учитываемого числа членов в разложениях и числа последовательных приближений на одном шаге.
появляется при учете релятивистских членов и негравитационных эффектов). Метод дает возможность вести вычисления с различной точностью в зависимости от учитываемого числа членов в разложениях и числа последовательных приближений на одном шаге.
Интересно получить ответ на вопрос, какая часть ошибки прогноза на 2029 г. и на 2036 г. может быть связана с ошибками численного интегрирования. Представление об этом дают «ошибки замыкания», вычисляемые при интегрировании уравнений движения Апофиса на различных интервалах времени при задании различных порядков интегрирования. Под ошибкой замыкания понимается модуль разности между исходным значением гелиоцентрического радиуса-вектора астероида и его окончательным значением в тот же самый момент, если интегрирование выполняется от исходной эпохи до конечной, а затем назад к исходной. Исследование было выполнено на трех интервалах: 1) от 2007 г. до 12 апреля 2029 г. (до входа Апофиса в сферу действия Земли); 2) от 2007 г. до момента наибольшего сближения Апофиса с Землей в 2029 г.; 3) от 2007 г. до 2036 г. Оказалось, что выбор порядка интегрирования слабо влияет на достигаемую точность. На первом интервале ошибка замыкания не превышает или равна 10 -11а.е., что вполне достаточно для сравнения вычисляемых положений с наблюдаемыми не только для оптических, но и для радиолокационных наблюдений. Погрешность вычисления геоцентрического расстояния астероида, зависящая от численного интегрирования, на границе сферы действия (до сближения в 2029 г.) составляет 2 × 10 -5км. Точность вычислений заметно снижается при тесном сближении (второй интервал). Ошибка замыкания возрастает до 10 -8а.е., но минимальное расстояние от Земли вычисляется с точностью до 30 см (ошибка, зависящая только от численного интегрирования). Наконец, к концу третьего интервала после сближения в 2029 г. координаты астероида вычисляются с ошибками порядка нескольких километров, а ошибка замыкания на этом интервале возрастает до 10 -7а.е. Таким образом, численное интегрирование не вносит существенных ошибок в вычисляемые положения на рассматриваемых интервалах.
7.4. Траектория сближения тела с Землей и другими массивными телами. Гравитационный маневр. Радиус захвата. Плоскость цели
Читать дальше
Конец ознакомительного отрывка
Купить книгу

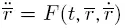 (зависимость правых частей от
(зависимость правых частей от 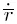 появляется при учете релятивистских членов и негравитационных эффектов). Метод дает возможность вести вычисления с различной точностью в зависимости от учитываемого числа членов в разложениях и числа последовательных приближений на одном шаге.
появляется при учете релятивистских членов и негравитационных эффектов). Метод дает возможность вести вычисления с различной точностью в зависимости от учитываемого числа членов в разложениях и числа последовательных приближений на одном шаге.










