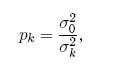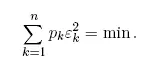Борис Шустов - Астероидно-кометная опасность - вчера, сегодня, завтра

Подводя итог, важно обратить внимание на то, что элементы истинной орбиты тела остаются неизвестными. Любая точка внутри доверительного эллипсоида представляет некоторую орбиту, совместимую с имеющимися наблюдениями. Однако вероятность того, что реальная орбита находится в малой окрестности номинального решения, является максимальной по сравнению с другими возможными решениями.

Отметим, что до сих пор мы рассматривали все наблюдения как имеющие одинаковую точность. На практике приходится определять элементы орбиты на основе рядов наблюдений, выполненных с различными точностями (имеющими различные среднеквадратичные ошибки σ 1, σ 2…, σ n). В таких случаях вводят понятие веса наблюдения, определяя его как

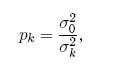
где σ 0 — произвольное положительное число.

Решение системы условных уравнений в таком случае ищут исходя из обобщенного принципа Лежандра: решение системы должно минимизировать взвешенную сумму квадратов остающихся невязок:

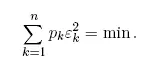
Из этого требования вытекает правило преобразования системы условных уравнений и ее решения: каждое условное уравнение должно быть умножено на корень квадратный из веса соответствующего наблюдения. После этой операции (так называемого приведения к равноточным наблюдениям) система решается так же, как в случае наблюдений, имеющих одну и ту же среднюю ошибку.

После того как номинальная орбита астероида определена, появляется возможность предвычислить его движение в предстоящий период времени и определить, угрожает ли Земле столкновение с ним в обозримом будущем. В зависимости от точности найденной орбиты такие расчеты желательно выполнять для всех АСЗ на интервалах от нескольких лет до нескольких десятков лет, а иногда и до нескольких сотен лет. Прогнозирование движения выполняется методом численного интегрирования уравнений движения, в которых учитываются члены, обусловленные притяжением больших планет и наиболее массивных астероидов (в случаях, требующих особой точности, иногда учитываются возмущения от трехсот наиболее массивных астероидов, см. раздел 7.3). В ходе численного интегрирования фиксируются моменты тесных сближений с Землей и другими большими планетами, которые могут заметным образом трансформировать орбиту тела и тем самым оказать влияние на ее последующие сближения с Землей.

Поскольку столкновения достаточно крупных тел с Землей — весьма редкие события, то при прогнозировании движения тела по номинальной орбите столкновения с Землей, как правило, не обнаруживаются. Нужно, однако, иметь в виду, что номинальная орбита является лишь одной из бесчисленного количества других возможных орбит, элементы которых более или менее близки к элементам номинальной орбиты. Фактическая орбита тела, которая нам не известна, находится где-то внутри области, ограниченной доверительным эллипсоидом (см. раздел 7.1).

Аналогичное представление об области неопределенности начальных условий движения справедливо и в том случае, если рассматривать точки не в пространстве элементов орбит, а в пространстве начальных значений прямоугольных координат и скоростей тел, что имеет несколько большую наглядность.

По мере увеличения числа использованных наблюдений и расширения покрываемого ими временного интервала, ошибки определения элементов, вообще говоря, уменьшаются, а вместе с тем сокращаются и полуоси доверительного эллипсоида. Его центр, соответствующий новому номинальному решению, при этом также несколько смещается в пространстве.

Каждая точка внутри доверительного эллипсоида соответствует некоторой возможной орбите. Тело на возможной орбите мы будем называть виртуальным ( возможным ) астероидом [Milani et al., 2002].

Если внутри доверительного эллипсоида случайным образом выбрать большое число виртуальных астероидов и следить за их движением на некотором интервале времени, то можно наблюдать, как с течением времени изменяются форма и размеры области пространства, в которой в данный момент заключены виртуальные астероиды. Во всех случаях, с которыми приходится иметь дело на практике, область, первоначально занятая доверительным эллипсоидом, постепенно расширяется и вытягивается вдоль номинальной орбиты тела. Причиной этого являются небольшие различия элементов орбит виртуальных астероидов, причем различие в среднем движении вызывает пропорциональные времени расхождения в средней аномалии, значение которой определяет положение тела на орбите. В результате граница области, занятой виртуальными астероидами, постепенно превращается в очень вытянутый эллипсоид, который можно представить в виде трубки более или менее постоянной ширины, окружающей номинальную орбиту. С течением времени длина трубки может достичь тысяч и миллионов километров и даже превзойти длину орбиты тела.