Борис Шустов - Астероидно-кометная опасность - вчера, сегодня, завтра

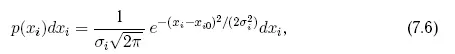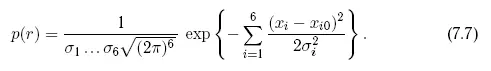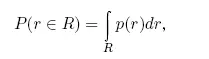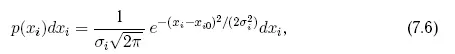
где под x iследует понимать элемент E i, p(x i) — плотность вероятности распределения ошибок соответствующего элемента, σ i — корень квадратный из дисперсии ошибок (среднеквадратичная ошибка i-го элемента).

Предположим ради простоты изложения, что случайные ошибки элементов E iи E jпопарно независимы, т. е. вероятность попадания ошибки элемента E iв некоторый интервал не зависит от ошибки элемента E j. В этом случае ошибки всех элементов являются независимыми в совокупности. Плотность вероятности одновременного попадания шести элементов в достаточно малую окрестность точки (E 1…, E 6) в этом случае выражается как произведение плотностей вероятностей распределения ошибок отдельных элементов:

p(E 1…, E 6) = p 1(E 1)p 2(E 2)… p 6(E 6).

Каждый сомножитель в правой части последней формулы определяется формулой типа (7.5). Из этого вытекает, что плотность вероятности в точке r в случае шестимерного нормального распределения при сделанном предположении определяется формулой

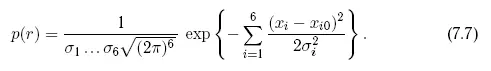
Указанная плотность вероятности остается неизменной во всех точках пространства, где

При любом положительном значении постоянной это выражение представляет собой уравнение эллипсоида в осях, совпадающих по направлению с главными осями эллипсоида и имеющих начало в точке (x 10, x 20, x 30…, x 60) шестимерного пространства. Если представить, что в шестимерном пространстве элементов по осям прямоугольной системы координат с началом в точке, отвечающей номинальной орбите, отложены величины σ iи представить себе шестимерный эллипсоид с полуосями σ i, то плотность вероятности на таком эллипсоиде будет всюду одинаковой. То же самое будет справедливо и для любого другого подобного и подобным образом расположенного эллипсоида. Такие эллипсоиды называются эллипсоидами равных плотностей вероятностей.

По аналогии с одномерным случаем можно заключить, что вероятность попадания точки внутрь некоторого эллипсоида равна интегралу

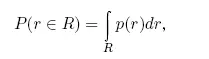
где интегрирование распространяется на все пространство, ограниченное эллипсоидом. Если полуоси эллипсоида неограниченно увеличиваются, то интеграл по всему пространству равен единице. Если представить эллипсоид с полуосями, равными 3σ i, то вероятность попадания точки в область пространства, ограниченную этим эллипсоидом, близка к единице (0,9973 6). Такой эллипсоид будем называть доверительным .

Выше предполагалось, что ошибки элементов независимы. На самом деле они корреляционно связаны. Отражением этих связей между ошибками отдельных элементов, найденных по методу МНК, являются величины недиагональных элементов обратной матрицы Q -1, которую называют корреляционной матрицей решения или матрицей ковариаций. Корреляционные связи могут проявляться по-разному. Примером двух элементов, находящихся в жесткой корреляционной зависимости, являются долгота узла и угловое расстояние перигелия от узла при малом наклоне орбиты. Ошибки этих величин близки по величине и противоположны по знаку.

Сделанное выше допущение о независимости случайных ошибок элементов эквивалентно допущению, что все недиагональные элементы матрицы ковариаций равны нулю. В том случае, если это допущение неверно, плотность вероятности многомерного нормального распределения будет иметь более сложный вид по сравнению с (7.7). В показателе экспоненты будет присутствовать сумма не только квадратов, но и смешанных членов вида (x i — x i0)(x j — x j0) с коэффициентами, зависящими от недиагональных элементов матрицы ковариаций (коэффициентов корреляции). Приравнивание суммы в показателе экспоненты к положительной постоянной дает уравнение эллипсоида равной плотности вероятности, но в этом случае ориентация главных осей эллипсоида не совпадает с ориентацией координатных осей. Путем поворота координатных осей уравнение эллипсоида может быть приведено к виду (7.8), в котором отсутствуют смешанные члены.

Корреляционные матрицы, определяющие погрешности элементов и корреляционные связи между ними, находят важное применение при определении погрешностей различных функций этих элементов. Этот вопрос еще будет обсуждаться в следующих параграфах.