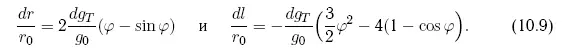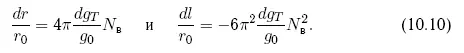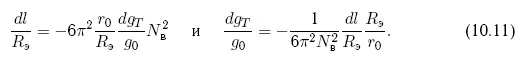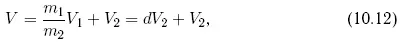Борис Шустов - Астероидно-кометная опасность - вчера, сегодня, завтра

В заключение данного раздела рассмотрим случай непрерывно действующей тяги dg Tпо оси T, которая оказывается наиболее результативной. Вектор тяги, направленный вдоль орбиты, создает ускорение, вызывающее изменение периода обращения угрожающего тела, нарастающее со временем. Теперь орбита будет представлять собой разворачивающуюся спираль (рис. 10.6).

Следовательно, появится линейный вековой уход астероида по координате S и квадратично нарастающий — по координате Т. Соответствующий анализ дает соотношения:

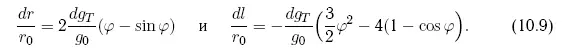
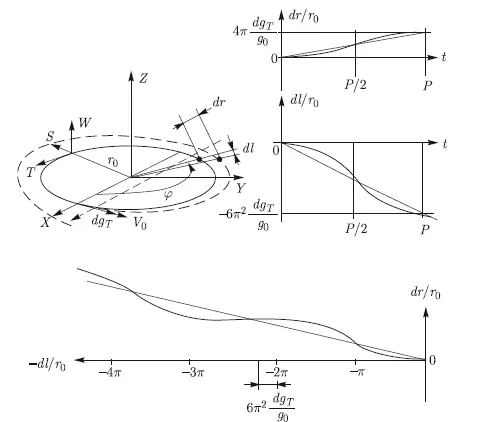
Рис. 10.6. Результат длительного воздействия постоянной тяги dg T, приложенной по оси T

Из этих соотношений получим величины вековых уходов за N ввитков:

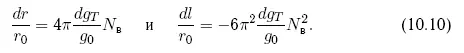
Таким образом, наиболее существенен и эффективен увод по оси T. Увод нарастает линейно по радиус-вектору и квадратично — по нормали. В результате получаем прогрессивно нарастающее относительное отставание от первоначального положения угрожающего астероида. Применяя прежнюю удобную нормировку, получим выражения для увода вдоль орбиты и требуемого ускорения:

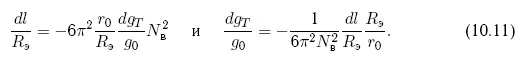
Обращаясь к примерам, получим, что для астероида Апофис в первом случае потребуется в течение одного витка создавать ускорение, равное dg T= 30 10 -6м/c 2, и тягу, составляющую ∼ 10 кгc. Для второго случая потребная тяга при тех же остальных условиях окажется равной ∼ 5 гс. Последний пример является иллюстрацией возможности увода с помощью весьма малых реактивных сил, например способом гравитационной буксировки.

Выше была проанализирована эффективность приложения импульса скорости к небесному телу. В литературе по проблеме космической угрозы делались, да и сейчас делаются предложения о создании такого импульса с помощью удара по угрожающему астероиду. При этом в качестве ударяющего тела предполагалось использовать космический аппарат. При ударе по астероиду космический аппарат передает определенное количество движения астероиду, что изменяет скорость астероида и, следовательно, его траекторию. Имеет смысл напомнить очень простые соотношения, описывающие соударения двух тел и сопутствующие соображения.

В качестве иллюстративных моделей можно выбрать случай абсолютно неупругого удара и его противоположность — случай абсолютно упругого удара. Сначала для простоты будем считать, что тела имеют идеальную сферическую форму, а удар — центральный (т. е. векторы скоростей тел направлены по линии, соединяющей центры тел).

Абсолютно неупругим ударом называют такой удар, после которого скорости обоих соударяющихся тел оказываются одинаковыми. В случае абсолютно неупругого удара космический аппарат, ударяющий по астероиду со значительной относительной скоростью, доходящей до десятков км/с, просто внедряется в небесное тело, поглощается им и продолжает дальнейшее движение совместно с ним. Разумеется, удар на таких скоростях вызывает значительные побочные эффекты, однако к их рассмотрению целесообразно обратиться несколько позже. Если абсолютно неупругий удар централен (рис. 10.7 а ), то, как известно из механики соударяющихся тел (см., например, [Хайкин, 1947]), при естественном здесь и далее предположении m 1 ≪ m 2имеем простое выражение для скорости астероида V после удара:

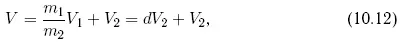
где V 1и V 2 — соответсвенно скорости ударника и астероида до удара, V — скорость общего тела (астероид + ударник) после удара, dV 2 — изменение скорости астероида после удара.

В случае нецентрального удара (рис. 10.7 б ) необходимо разложить обе скорости на составляющие V n1и V n2в направлении линии, соединяющей центры шаров, и составляющие V t1, V t2 — в перпендикулярном направлении (чтобы не загромождать рисунок, составляющие скоростей не показаны). Для составляющих V n1и V n2все будет обстоять точно так же, как и при центральном ударе, хотя очевидно уменьшение изменения скорости астероида. Составляющие V t1, V t2вызовут вращение астероида, дополняющее его первичное движение относительно центра масс.