Борис Шустов - Астероидно-кометная опасность - вчера, сегодня, завтра

Оценки величины зоны разрушений ударными волнами, вызванными падениями астероидов и комет, были даны в работе [Chapman and Morrison, 1994]. Авторы принимали во внимание избыточное давление на фронте ударной волны и динамическое давление, которое вызвало падение деревьев. Для калибровки они использовали Тунгусское событие [Зоткин, Цикулин, 1966], где ударные волны вызвали падение деревьев на площади 2000 км 2, которая эквивалентна площади круга с радиусом R s= 25 км. Предполагалось, что площадь A sсильных повреждений строений приблизительно равна площади вывала леса. Для оценок может быть использовано следующее выражение:

A s= πR 2s = 200E 2/3k, Rs = 8E k 1/3,

где радиус R sвыражен в километрах, площадь A s — в квадратных километрах, энергия ударяющего тела E k — в мегатоннах. Коэффициенты в формуле изменяются с высотой взрыва. «Оптимальная» высота h [км] составляет 6,4E 1/3[Glasstone and Dolan, 1977; Hills and Goda, 1993]. Если высота взрыва уменьшается до нуля, радиус R sуменьшается приблизительно в 1,4 раза. Для E = 30 Мт получается радиус R s= 18 км.

Прорыв атмосферы. Законы подобия, которыми мы пользовались для оценок, основаны на теоретических исследованиях гидродинамической задачи о распространении ударной волны после точечного взрыва в однородной атмосфере и на исследованиях с помощью численного эксперимента распространения взрывных волн, образованных химическими взрывами с высокой энергией и ядерными взрывами с энергиями менее 10 Мт. Но для больших энергий радиус R sоказывается порядка характерной высоты атмосферы или превышает ее (для E = 10 3Мт мы получаем R s= 80 км), поэтому оценки следует уточнять численными расчетами.

Двумерные численные расчеты взрыва в неоднородной атмосфере и различные теоретические оценки прорыва атмосферы показывают, что ударная волна вследствие уменьшения плотности воздуха с высотой над поверхностью Земли движется вверх быстрее, чем в радиальном направлении. Численные расчеты [Jones and Sanford, 1977; Jones and Kodis, 1982] взрыва с энергией 500 Мт, произведенного на поверхности, показали, что динамическое давление превосходит порог вывала леса на расстояниях в 27,5 км вместо 45 км, как это следует из закона подобия. В действительности давление и скоростной напор снижаются еще больше за счет влияния следа, не учтенного в этих расчетах.

Результаты расчета для большого тела (диаметром 10 км) приведены на рис. 8.3. Картина распределения плотности и температуры в более поздние моменты времени показана на рис. 8.4. Хотя след здесь также присутствует, но выброс вверх в основном облегчен за счет быстрого падения плотности атмосферы с высотой.

8.1.3. Световой импульс и пожары.Падение Тунгусского космического тела 30 июня 1908 г. вызвало пожар на площади около 500 км 2[Vasilyev, 1998], что в 4 раза меньше, чем площадь опустошения леса взрывными волнами (2000 км 2). Этот пожар наглядно демонстрирует роль светового излучения. В Хиросиме и Нагасаки 20–30 % всех жертв были ранены за счет ожога от прямого действия теплового излучения вспышки. Используя эти данные, можно ожидать, что лучистое воздействие при энергии взрыва в 10–30 Мт могло бы быть причиной ожогов незащищенной кожи первой степени (обратимое повреждение) для 82 % населения, а 15 % получили бы ожоги второй степени (которые можно вылечить за одну или две недели) [Glasstone and Dolan, 1977]. Конечно, жертвы прямого действия теплового излучения вне зоны «огненного шара» могут быть сокращены простыми способами гражданской обороны (убежище и другие меры защиты) при условии предупреждения о возможном падении космического объекта. Мы должны упомянуть также глазные травмы, вызывающие слепоту и ожоги сетчатки, но они также могут быть сокращены адекватной тренировкой использования специальных фильтров для глаз, опять же при условии предупреждения об опасности.

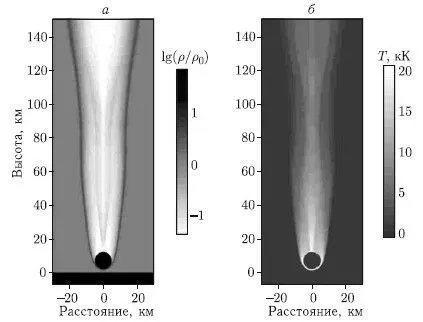
Рис. 8.3. Распределение относительной плотности ( а ) и температуры ( б ) непосредственно перед столкновением каменного тела диаметром 10 км с поверхностью Земли

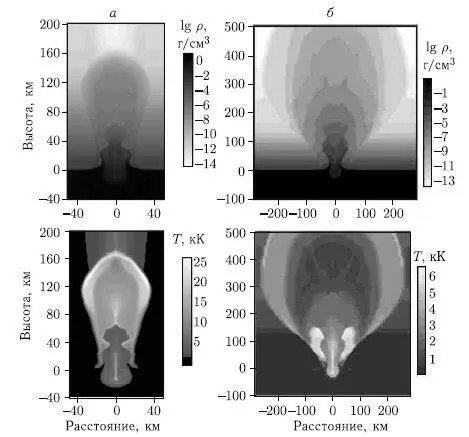
Рис. 8.4. Распределение плотности (верхняя панель) и температуры (нижняя панель) через 5 с ( а ) и 15 с ( б ) после удара о Землю каменного тела диаметром 10 км со скоростью 20 км/с

Используя «экспериментальное» значение площади пожара для энергии E = 30 Мт (Тунгусское событие), получим следующие соотношения: