Джеймс Гордон - Почему мы не проваливаемся сквозь пол

Рис. 27. Схематическое изображение сдвига, происходящего путем скольжения целой плоскости атомов без помощи дислокационных механизмов.

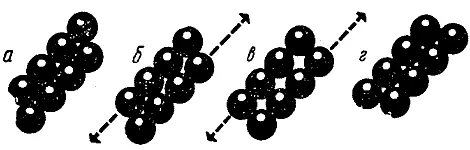
На рис. 27 изображена двумерная модель - два параллельных ряда монет, лежащих на столе. Ясно, что последнее сопротивление сдвигу исчезает в момент, когда атомы- монеты балансируют на вершинах друг у друга; такое положение создается в момент, когда слой оказывается сдвинутым относительно другого слоя на угол 30°. Пройдя эту точку, атомы будут сваливаться в положение равновесия на дне следующей ямы, и сдвиг на одно межатомное расстояние будет завершен. Сопротивление сдвигу началось с нуля, возросло до некоторого максимума, затем снова упало до нуля, когда атомы оказались на вершинах. Сопротивление будет максимальным примерно на полпути к вершине, в нашем случае это соответствует углу сдвига около 15°. Трехмерный случай будет немного более сложным, для него максимум наступает при 10°. Для кристаллов, которые состоят из атомов различных размеров, этот угол может быть еще меньше.

Очень грубые вычисления, основанные на этой модели, дают величину теоретической прочности на сдвиг порядка 10% от модуля упругости Е . (Более сложный расчет, проведенный А. Келли, дает 5–10% от Е .) Впрочем, не слишком большая точность этих чисел особого значения не имеет: при обычных испытаниях реальных материалов мы достигаем их весьма редко [28] Заметим, что теоретическая прочность на сдвиг, вообще говоря, ниже, чем прочность на разрыв. Поэтому, если образцы, близкие к совершенным, могут достичь очень высоких напряжений, они разрушаются преимущественно путем сдвига. Это мы видели в случае стекла. . Теоретическое значение прочности на сдвиг для железа составляет около 1200 кг/мм 2, но практически кристалл очень чистого железа сдвигается при напряжениях, лежащих между 1,5 и 8,0 кг/мм 2, для рядовых сталей прочность на сдвиг составляет 15–25 кг/мм 2, для самых прочных сталей - около 150 кг/мм 2.

Очень мягкие металлы, например чистые золото, серебро, свинец, можно испытывать на сдвиг руками. После сильного наклепа сопротивление сдвигу несколько повышается, но оно никогда не приближается к теоретической величине. Широко известна ковка металла, которая делает его более твердым: таким путем повышали твердость кромок еще медного и бронзового оружия, а в старину часовых дел мастера всегда обрабатывали так латунные заготовки шестеренок. (Если вы воздержитесь от смазки шестеренок старинных напольных часов, то зубья их не только перестанут собирать пыль и быстро истираться, но с течением времени будут становиться тверже и полироваться, и так будет продолжаться века.)

Вплоть до 1934 года общепринятое объяснение всех этих явлений было крайне неубедительным и походило на желание уйти от вопроса. Вот оно: "Скольжение происходит вследствие того, что малые кусочки кристалла, обламываясь, работают как подшипники качения. Когда их становится слишком много, они начинают мять друг друга, и это является причиной наклепа" . Как говорил герцог Веллингтон, "если вы верите в это, вы можете поверить во что угодно".

В 1934 году Дж. Тэйлор из Кэмбриджа, который изобрел лемешный якорь, придумал также дислокацию. По крайней мере, он "посадил" дислокацию в научную статью как гипотезу. Основная идея была чрезвычайно проста, настолько проста, что не могла быть ошибочной. И она в самом деле оказалась верной.

Почти невероятно, рассуждал Тэйлор, что металлические кристаллы в действительности так совершенны, как мы о них думаем, когда вычисляем их прочность. Давайте предположим, что во всем объеме кристалла, быть может, через каждый миллион атомов или что-нибудь около этого, встречаются небольшие неправильности. При этом нас интересуют не точечные искажения, такие, как чужеродные атомы, которые могут обеспечить движение отдельных точек, а линейные дефекты, которые позволят продвинуться вперед целым армиям атомов на широком фронте.

Кристалл состоит из слоев, или плоскостей атомов, которые показались бы наблюдателю, уменьшенному до размеров электрона, громоздящимися в ужасающей бесконечной регулярности, подобно страницам какой-то громадной книги. Предположение Тэйлора заключалось в том, что кое-где слой атомов оказывается незавершенным, как если бы кто-то вставил лишний лист бумаги между страницами книги и теперь она в одних местах состоит, положим, из миллиона страниц, а в других - из миллиона и одной страницы. Самые интересные явления разыгрываются, конечно, вдоль линии, где лишний слой атомов подходит к концу, на кромке "лишней" плоскости. Посмотрев на рис. 28, а , мы увидим, что должны быть две области, по обе стороны от кромки экстраплоскости, где атомы сдвинуты на угол, примерно соответствующий теоретической прочности кристалла на сдвиг. Другими словами, в этих зонах кристалл практически разрушен.