Джеймс Гордон - Конструкции, или почему не ломаются вещи

Вспомним теперь, что главные артерии, такие, как артерии ног, могут иметь диаметр где-то около сантиметра, а длину около метра. Если упомянутые деформации действительно относились бы как два к одному, то, как показывает простой расчет, изменению диаметра артерии на 0,5 мм, которое без труда "умещается" в организме, соответствовало бы изменение длины на 25 мм.

Очевидно, что такого порядка изменения длины с частотой 70 раз в минуту невозможны и их на самом деле нет. Если бы такое происходило, наше тело вообще не могло бы функционировать. Достаточно только представить себе, что такое происходит с сосудами мозга.

К счастью, на самом деле продольные удлинения в находящихся под давлением трубах всех видов и размеров много меньше, чем можно было бы ожидать или опасаться. Доказательством того, что дело обстоит именно таким образом, является так называемый коэффициент Пуассона.

Если вы натянете резиновую ленту, она станет заметно тоньше, то же самое происходит и со всеми другими твердыми телами, хотя для большинства материалов это не так бросается в глаза. Напротив, если вы уменьшите длину куска материала, сжав его, поперечные размеры увеличатся. И то и другое происходит благодаря действию упругих сил, и первоначальная форма тела восстанавливается при снятии нагрузки.

Мы не замечаем этих поперечных перемещений в таких веществах, как сталь или кость, в силу малости как продольной, так и поперечной деформаций, но фактически и здесь дело обстоит точно так же. То обстоятельство, что подобные эффекты характерны для всех твердых тел и такое поведение существенно для практических задач, было впервые отмечено французом С.Д. Пуассоном (1781-1840). Он родился в очень бедной семье и в детстве не получил сколько-нибудь систематического образования, но в возрасте тридцати одного года стал академиком, а во Франции это одна из наивысших почестей, и он удостоился ее за свои работы в области теории упругости. Как было сказано в гл. 2, закон Гука гласит, что модуль Юнга = E = (напряжение / деформация) = s/e .

Поэтому, если мы приложим к плоской пластинке растягивающее напряжение s 1 , она удлинится упругим образом, так что в направлении растяжения деформация будет иметь величину e 1 = s 1 / E .

Однако, кроме того, пластинка сократится в поперечном направлении (то есть в направлении под прямым углом к напряжению s 1 ), и величину соответствующей деформации мы обозначим e 2 . Пуассон обнаружил, что для каждого материала отношение деформаций e 1 и e 2 есть величина постоянная, и это отношение теперь принято называть коэффициентом Пуассона. Ниже мы всюду будем использовать для этой величины обозначение ν. Таким образом, для данного материала, подвергаемого простому одноосному нагружению напряжением s 1 , ν= e 2 / e 1 = коэфициент Пуассона [50] Поскольку деформация e 2 всегда имеет знак, противоположный знаку деформации e 1 , коэффициент Пуассона ν обязан быть отрицательным и выражаться числом со знаком минус. Однако знак минус мы будем опускать. В вычислениях, которые мы будем делать, это будет компенсировано нужным выбором знака в соответствующих формулах.

Деформацию e 1 в направлении напряжения s 1 можно назвать первичной деформацией, а деформацию e 2 , вызванную напряжением s 1 в перпендикулярном ему направлении, - вторичной деформацией (рис. 55). Согласно этому, e 2 = ν e 1 , а так как e 1 = s 1 / E (это - закон Гука), то e 2 = ν s 1 / E .

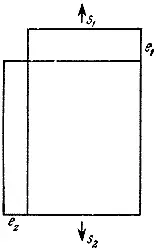
Рис. 55. При одноосном нагружении твердого тела растягивающим напряжением s 1 тело испытывает в направлении этого нагружения деформацию e 1 , а в поперечном направлении сокращается, при этом деформация равна e 2 .

Таким образом, если мы знаем значения величин νи E , мы можем вычислить и первичную, и вторичную деформации.

Для материалов, используемых в технике, таких, как металлы, камень и бетон, значения νлежат всегда между 1/4 и 1/3. Для твердых биологических материалов значения коэффициента Пуассона обычно выше, и часто они лежат вблизи 1/2. Преподаватели элементарной теории упругости сказали бы вам, что коэффициент Пуассона не может принимать значений больше 1/2, иначе происходили бы разного рода абсурдные и неприемлемые вещи. Это справедливо лишь отчасти, и значения коэффициента Пуассона для некоторых биологических материалов являются очень высокими, часто они больше единицы [51] Чтобы избавить негодующих специалистов от лишней переписки, замечу, что мне хорошо известно о связанных с этим энергетических аспектах. Такие аномалии имеют разумное объяснение. . Экспериментальное значение коэффициента Пуассона для моего живота, измеренное недавно мною в ванне, составляет примерно единицу (см. сноску выше).