Джеймс Гордон - Конструкции, или почему не ломаются вещи

Это стандартная инженерная формула.

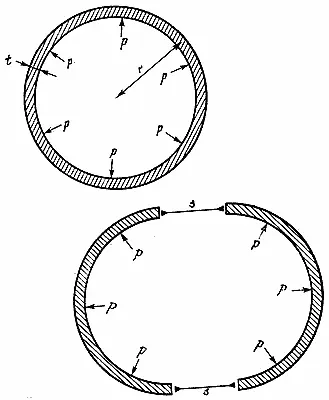
Рис. 26. Сосуд высокого давления сферической формы. Внутреннее давление p , средний радиус сосуда r и толщина стенки t .

Рис. 27. Схематический разрез сосуда высокого давления. Представим себе, что сосуд разрезан пополам. Равнодействующая сил давления, действующего внутри каждой из половинок оболочки, должна уравновешиваться напряжениями, действующими на поверхности разреза. Площадь этой поверхности равна 2 π rt .

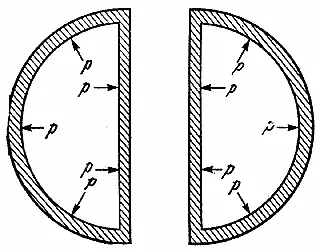
Рис. 28. Равнодействующая сил давления, действующего на поверхность полусферы, равна силе давления, действующей на плоский диск того же диаметра, которая имеет величину π r 2p . Следовательно, напряжениеs = (нагрузка / площадь) =( π r 2p ) / ( 2 π rt ) = rp/2t

Сферические сосуды находят свое применение в технике, но более широко используются сосуды цилиндрической формы, особенно в виде труб. Поверхность цилиндра не обладает такой симметрией, как поверхность сферы, и поэтому мы не можем предположить, что напряжение, действующее в направлении оси цилиндра, и напряжение, действующее в направлении его окружности, одинаковы; они и на самом деле неодинаковы. Обозначим s 1 напряжение в оболочке цилиндра в осевом направлении и s 2 - в окружном направлении.

Из рис. 29 видно, что напряжение s 1 - осевое напряжение в оболочке - должно быть таким же, как и у сферического сосуда, то есть s 1 = rp/2t.

Чтобы получить величину окружного напряжения s 2 , мысленно разрежем цилиндр в другой плоскости, как показано на рис. 30; это позволит заключить, что s 2 = rp/t .

Таким образом, окружное напряжение в стенках цилиндрического сосуда высокого давления равняется удвоенному осевому напряжению, то есть s 2 = 2s 1 (рис. 31). Одно из следствий этого мог наблюдать каждый, кто хоть однажды отваривал сосиски. Когда содержимое сосиски чрезмерно разбухает и шкурка лопается, разрыв всегда бывает продольным. Иными словами, шкурка разрывается вследствие действия окружного, а не осевого напряжения.

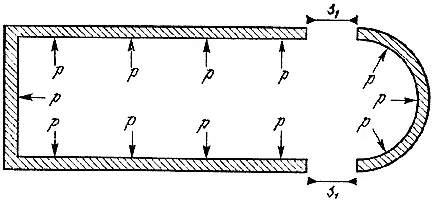
Рис. 29. Продольное напряжение s 1 в оболочке цилиндрического сосуда высокого давления равно напряжению в эквивалентном сферическом сосуде: s 1 = rp/2t .

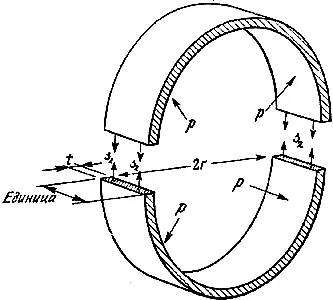
Рис. 30. Окружное напряжение в цилиндрическом сосуде s 2 = rp/t .

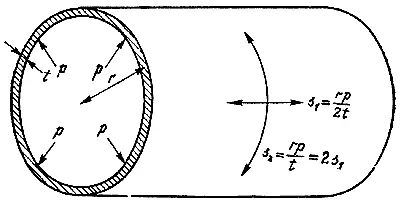
Рис. 31. Напряжение в стенках цилиндрического сосуда высокого давления

Эти формулы постоянно в ходу не только в инженерном деле, но и в биологии. Их используют для вычисления прочности труб, котлов, воздушных шаров, куполов крыш с воздушной поддержкой, ракет и космических кораблей. Как мы увидим в гл. 7, с этим же простым разделом теории целиком связан вопрос о постепенном превращении амебообразных существ в удлиненные и более подвижные примитивные создания.

Другим следствием проделанных нами расчетов является то, что при необходимости удерживать при данном давлении данное количество жидкости потребуется цилиндрический сосуд большего веса, чем сферический. Там, где весовой фактор весьма существен, как в кислородных баллонах, которые берет с собой на большую высоту альпинист, или в баллонах стартовых ускорителей самолета, сферическая форма является обычной. В большинстве же других случаев, где вес не так важен, используются контейнеры цилиндрической формы как более дешевые и удобные, например газовые баллоны, используемые в быту, в больницах, гаражах.