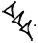Генри Саггс - Величие Вавилона. История древней цивилизации Междуречья

Применительно к вавилонским числительным неопределенность может проявляться в следующих формах: в записи

вертикальные клинья могут предназначаться для представления или «единиц», или «шестидесяток», а четыре широких клина – или «шестидесяток», или «единиц». Поэтому такой знак обычно может означать в наших терминах

или (2 Ч 60) + 40, то есть 160,

или 2 + 40 / 60, то есть 2 2/3.

Вторая неопределенность заключается в том, что две группы клиньев могут не означать последовательных свойств шестидесятеричной системы, иными словами, в клинописи, приведенной выше, если четыре широких клина представляют просто сорок единиц, два вертикальных клина могли представлять не 2 Ч 60, а 2 в следующей, более высокой степени, а именно 2 Ч 60 2= 2 Ч 3600.

тогда будет выражать 7200 + 40 = 7240. В ранний период неопределенность иногда ликвидировалась написанием числа с двумя элементами, далеко отстоящими друг от друга, когда они не выражают последовательные степени 60. Так, 7240 = (2 Ч 60 Ч 60) + (0 Ч 60) + (40 Ч 1), что могло быть записано так:

Однако так делалось не всегда.

В период Селевкидов в таких случаях использовался специальный знак зеро —

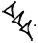
Очевидно, что в такой системе могут возникать ошибки, что, безусловно, и происходило время от времени. Следует, однако, заметить, что профессор Нойгебауэр, крупнейший современный авторитет в области вавилонской математики, однажды признался, что сделал больше ошибок при проверке древних вычислений, чем писцы в оригинальных документах.

Математические тексты, с которыми мы знакомы, принадлежат к двум отдельным периодам, разделенным между собой тысячелетием или даже больше. Более ранняя и крупная группа дошла до нас из старовавилонского периода, вторая – из периода Селевкидов, то есть после 300 г. до н. э.

Считалось, что за относительно продвинутой старовавилонской математикой лежит долгий период постепенного развития. Однако убедительных доказательств этой гипотезы нет. Нойгебауэр справедливо указывает, что во всех периодах математического прогресса, которые нам известны, бурное развитие наблюдалось в течение века или около того между двумя периодами стагнации.

Полезно еще раз подчеркнуть, что подавляющее большинство сотен тысяч клинописных табличек имеют экономическое содержание и касаются таких прозаических вещей, как расписки, займы и нормы. Чисто математических текстов значительно меньше. В них имеются задачи и таблицы. Задачи – это описание алгебраических или геометрических задач, а табличные тексты содержат таблицы для умножения, деления и подсчета обратных величин, квадратов, квадратных корней, кубов, кубических корней и т. д. Многие табличные тексты, большинство из которых найдены в Ниппуре, очевидно, являлись школьными упражнениями. Об этом свидетельствует тот факт, что на некоторых табличках одна и та же таблица повторяется, выполненная разными людьми. На других табличках можно видеть на одной стороне математические таблицы, на другой стороне – словари (широко использовавшиеся для обучения писцов). Известно, что Ниппур был развитым центром обучения писцов в старовавилонский период, а математика, безусловно, входила в программу обучения.

Что касается уровня вавилонских математических достижений старовавилонского периода (ок. 1800 до н. э.), Нойгебауэр сравнивает его с ранним Ренессансом. В основном речь шла об алгебре, но уже были известны свойства элементарных последовательностей, таких как арифметическая и геометрическая прогрессия, а также некоторые геометрические отношения. Сегодня ясно, что сущность того, что мы называем теоремой Пифагора – в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, – было известно уже в Вавилоне. Правда, нет никаких доказательств того, что вавилоняне могли доказать эту теорему. Хотя некоторые авторы считают, что одна старовавилонская табличка, покрытая геометрическими чертежами (см. фото 34 и 35), связана с теоретическим доказательством отношения между площадями разных фигур, вавилонская математика (как и вся вавилонская наука) по большей части основывалась на эмпирических знаниях, а не на формальных доказательствах. Величина числа π была известна очень точно – 3 1/8, то есть с точностью до 0,6 процента. Этому можно противопоставить ситуацию в Израиле во времена Соломона, то есть тысячелетием позже, где число π считали равным 3. Квадратные уравнения, включающие элементы до восьмой степени, были хорошо известны, и, как уже отмечалось, существовали таблицы квадратных и кубических корней.