Джон Готтман - Как сохранить любовь в браке

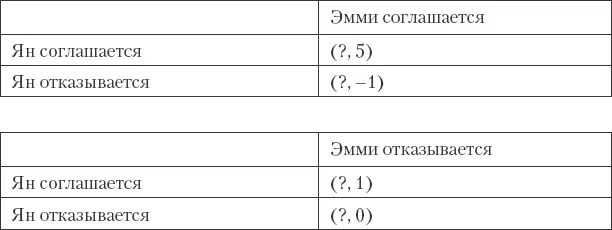
Мы можем вычислить точку безразличия для Яна с помощью приведенных ниже матриц:

И:

ЕР для Яна Эмми соглашается= 5σ Соглашается+ (–1) (1 – σ Соглашается).

ЕР для Яна Эмми отказывается= 1σ Соглашается+ (0) (1 – σ Соглашается).

Пусть ЕР для Яна Эмми соглашается= ЕР для Яна Эмми отказывается; точка безразличия Яна.

5σ Соглашается– 1 +σ Соглашается= σ Соглашается.

5σ Соглашается= 1.

σ Соглашается= 1/5.

Эмми будет соглашаться на секс только в 1/5 всех случаев и отказываться в 4/5 случаев, чтобы Ян был безразличен к ее смешанной стратегии с точки зрения ее ожидаемых выигрышей. А как насчет его смешанной стратегии?

ЕР Ян соглашается= 5σ Соглашается+ (– 1) (1 – σ Соглашается).

ЕР Ян отказывается= 1σ Соглашается+ (0) (1 – σ Соглашается).

Пусть ЕР Ян соглашается= ЕР Ян отказывается; точка безразличия Эмми.

5σ Соглашается– 1 + σ Соглашается= σ Соглашается

σ Соглашается= 1/5

Если Ян использует смешанную стратегию, соглашаясь на секс в 1/5 случаев и отказываясь в 4/5, Эмми будет безразлична к этому с точки зрения ее выигрышей. Прекрасно, мы получили уравнение Нэша для смешанной стратегии. Ура!

Но как часто у этой пары на самом деле будет секс, если исходить из этой матрицы выигрышей? Поскольку оба вынуждены соглашаться на занятия сексом, взаимный показатель согласия составит (1/5) × (1/5) = 1/25, то есть 0,04 или 4 %. При том что в году 365 дней, пара будет заниматься сексом 15 дней в году (примерно раз в три недели). Это удивительно низкий показатель для такой пары, потому что они разработали разумную с точки зрения психологии таблицу. Что происходит?

Теперь давайте поговорим о хорошем и иначе взглянем на исходную матрицу, составленную на основе теории игр. Пусть выигрыш за отказ от секса будет варьировать – переменная г.

Уравнения смешанной стратегии для Эмми будут выглядеть так:

5σ Соглашается+ (r) (1 – σ Соглашается) = (r) (σ Соглашается) + (0) (1 – σ Соглашается)

σ Соглашается(5–2r) = r

σ Соглашается= r/(5–2r)

Если мы задаем, что σ Соглашается= 0,5, то г должна быть – 1,25. Для Яна смешанная стратегия выглядит точно так же, поэтому если мы зададим г = 1,25, у пары будет секс с показателем частоты (1/2) × (1/2) = 0,25, а это значит, что при г = 1,25 партнеры будут заниматься сексом 91 раз в год – примерно 1,8 раза в неделю.

Этот результат очень близок к среднему национальному показателю. Если мы зададим г большее значение (что будет подразумевать больший выигрыш за отказ от секса), пара будет заниматься сексом еще чаще. Например, если г = 1,53, σ Соглашается= 0,80: Эмми соглашается на секс в 80 % случаев, поэтому партнеры будут заниматься сексом (0,8) × (0,8) × (365) = 233 дня в году, или примерно 4 раза в неделю. Такой результат для Яна и Эмми выглядит более многообещающим.

Эти результаты позволяют предположить, что, если пара хочет часто заниматься сексом, необходимо давать выигрыш, пусть и небольшой, даже если один из партнеров отказывается от него. Если партнер говорит «нет», он должен получать положительный выигрыш. Этот вывод может показаться удивительным, но он математически обоснован.

Я знаю, что многие люди сочтут эти выкладки запутанными и сложными, но решение, которое мы получили, нельзя назвать сложным. Анализ на основе теории игр предлагает парам, которые столкнулись с угасанием желания, простую стратегию. Если они сделают так, что ответ «не сегодня» будет считаться более приемлемым, их ждет много вечеров, когда оба скажут «да». И не понадобится никакой женской «Виагры». Вполне достаточно немного чуткости.

Почти всей моей трудовой деятельностью на протяжении последних сорока лет я обязан чудесному сотрудничеству с моим лучшим другом Робертом У. Левенсоном, который был шафером на моей свадьбе. Ничто не может сравниться с великим даром дружбы, любви и товарищества, который делал нашу жизнь богаче столько лет. Мы с Бобом наслаждаемся нашей глубокой и долгой дружбой, базирующейся на исследованиях и чувстве юмора. На каждом докладе я благодарю Боба за его вклад в работу. Однако эта книга была написана без пристального и прозорливого ока моего друга, поэтому я беру на себя всю ответственность за любые ошибки, содержащиеся в ней.