Дмитрий Сочивко - Расколотый мир. Опыт анализа психодинамики личности человека в экстремальных условиях жизнедеятельности

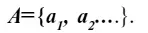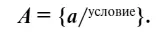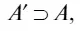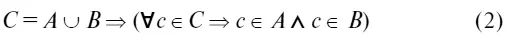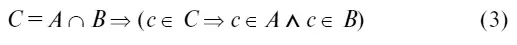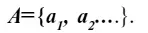
2) Множество может быть задано условием, позволяющим отличать его элементы среди всех других. В этом случае каждый элемент множества удовлетворяет заданному условию и ни один элемент, не принадлежащий данному множеству, не удовлетворяет указанному условию. Тогда применяется следующая запись:

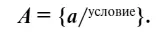
Итак, мы определили понятия множества и подмножества. Полезно также ввести понятия надмножества как множества, содержащего данное множество:

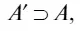
и понятие пустого множества, как множества, не содержащего ни одного элемента (обозначается ∅). Пустое множество по определению является подмножеством любого множества. Введем теперь понятие объединения множеств. Множество С является объединением множеств А и В , если каждый элемент С является либо элементом А , либо элементом В . В принятой символике это можно записать так:

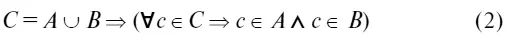
Аналогично можно определить понятие пересечения двух множеств. Множество С является пересечением множеств А и В , если каждый элемент С является одновременно и элементом А и элементом В , т. е. С есть множество общих элементов А и В . Если, однако, у А и В нет общих элементов, то С есть пустое множество. Это можно записать так:

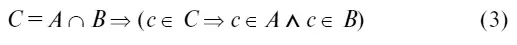
Если В является подмножеством А , то можно определить понятие разность множеств А и В , как множество тех элементов А , которые не являются одновременно элементами множества В .

Разность А и В называется также дополнением В в А . Введем теперь понятие пары объектов. Этими объектами могут быть как элементы множеств, так и сами множества. В понятии пары кроме количества выбираемых объектов фиксируется также порядок их следования. Так, например, если A ≠ В , то две пары множеств ( А, В ) и ( В, А ) не являются равными: ( А, В ) ≠ ( В, A ). Рассмотрим теперь множество всех пар элементов множества А , оно называется декартовым квадратом множества и обозначается А 2, Смысл такого названия в том, что если множество А содержит k элементов, то количество упорядоченных пар будет равно k 2.

Итак, декартов квадрат множества А сам является некоторым множеством. Любое его подмножество будем называть бинарным отношением, заданным на множестве А . (Отметим, что все другие виды отношений, которые можно определить на множестве А , также являются подмножествами, но уже не декартова квадрата А , а любой другой декартовой степени А , т. е. являются множествами троек, четверок и т. д. элементов из А .)

Так как понятие отношения является одним из важнейших понятий современной психологии, остановимся подробнее на уяснении смысла его точного определения, приведенного выше. Первое, что бросается в глаза, это то, что отношение является некоторым множеством. Это на первый взгляд противоречит тому смыслу, который вкладывается в понятие отношение в гуманитарных науках. На наш взгляд это противоречие является только кажущимся. Действительно, когда говорят об отношениях личности, отношениях между людьми, отношениях человека к тем или иным объектам внешнего мира, то создается впечатление, что выражение отношения не предполагает наличия какого-то множества, над которым это отношение можно было бы задать.

Определим теперь некоторые важные свойства отношений. Возьмем для примера отношение родства между людьми. Обозначим его буквой Р (людей будем обозначать маленькими буквами латинского алфавита). Первое, что можно сказать об этом отношении, это то, что человек не является родственником самому себе, т. е. аРа неверно. Такое отношение называется антирефлексивным. Если же отношение аРа – выполнено, т. е. пара ( а, а ) принадлежит Р , то такое отношение называется рефлексивным, т. е. обладает свойством рефлексивности. Например, отношение равенства является рефлексивным. Любой объект равен сам себе.