Великая русская культура изначально была основана на идее постоянного рефлексивного восхождения, одухотворенного идеями справедливости и человечности. Наверняка духовные муки Эйнштейна и Бора были навеяны именно ее величайшими представителями – Толстым и Достоевским. Ныне в мире все большее значение приобретают голоса сторонников и последователей Щедровицкого, Лефевра и Лепского, истинных основателей рефлексивного транснационального движения, рожденного в недрах этой могучей культуры.
Литература
1. Birshtein, B., Borsevici, V. (2002). Stratagems of Reflexive Control in Western and Oriental Cultures. International Interdisciplinary Scientific and Practical Journal ―Reflexive Processes and Control‖, vol 1, nr. 2. Moscow: "Kogito Center" Publishing House
2. Lepskiy, V.E. (2010) Reflexive and Active Environments of Innovative Development. – Moscow: "Kogito Center" Publishing House
В. В. Карюкин, Ф. С. Чаусов (Военный учебно-научный центр «Военно-Морская Академия», Санкт-Петербург) Рефлексивные игры противодействия
Аннотация . Рассматриваются рефлексивные игры при наличии признаков распознавания.
Ключевые слова : рефлексивные игры противодействия, признаки распознавания.
V. V. Karjukin, F. S. Chausov (Military educational and scientific center «Naval Academy»,St. Petersburg)
REFLEXIVE GAMES COUNTER
Abstract . Reflexivity games if there are signs of recognition.
Keywords : reflexive games, signs of recognition.
Задачи противодействия, рассматриваемые нами [1–3], характеризуются тем, что сначала делает выбор один из игроков, а второй игрок, чтобы не быть обреченным на поражение, должен разгадать выбор противника. Таковы, например, игра «нападение и оборона»[1], «игра в прятки»[4]. Изучение таких игр требует привлечения признаков распознавания стратегии противника. Данная задача требует привлечения теории рефлексивных игр [4].
Необходимые определения и обозначения. Рассмотрим игру, задаваемую матрицами:
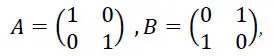
где первая матрица есть матрица выигрышей игрока 𝒜, а вторая дает выигрыши игрока ℬ. Игрок 𝒜 выбирает строчку (𝑖 ∈ 1,2), игрок ℬ – столбец (𝑗 ∈ 1,2). После того как выбор сделан, игрок 𝒜 получает выигрыш 𝑎 𝑖𝑗, а игрок ℬ – выигрыш 𝑏 𝑖𝑗. Матрицы известны обоим игрокам. Данная игра является игрой с постоянной суммой 𝑎 𝑖𝑗+ 𝑏 𝑖𝑗= 1, и ее равновесные смешанные стратегии одинаковы для обоих игроков 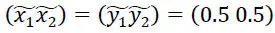 . Здесь введены обозначения: 𝑥 1, 𝑥 2– вероятности с которыми игрок 𝒜 выбирает первую (𝐴 1) или вторую (𝐴 2) стратегию (первую или вторую строчку матрицы 𝐴); аналогично (𝑦 1𝑦 2) – распределение вероятностей на стратегиях 𝐵 1,𝐵 2(столбцах матрицы 𝐵). Математическое ожидание выигрыша для игрока 𝒜 равно 0.5. Дополним описание данной игры допущением, что для каждой стратегии игроков известны признаки распознавания, известные обоим. Кроме того, для каждого такого признака существуют косвенные признаки, некоторые из которых носят рефлексивный характер. Будем считать, что скрытие косвенных признаков невозможно.
. Здесь введены обозначения: 𝑥 1, 𝑥 2– вероятности с которыми игрок 𝒜 выбирает первую (𝐴 1) или вторую (𝐴 2) стратегию (первую или вторую строчку матрицы 𝐴); аналогично (𝑦 1𝑦 2) – распределение вероятностей на стратегиях 𝐵 1,𝐵 2(столбцах матрицы 𝐵). Математическое ожидание выигрыша для игрока 𝒜 равно 0.5. Дополним описание данной игры допущением, что для каждой стратегии игроков известны признаки распознавания, известные обоим. Кроме того, для каждого такого признака существуют косвенные признаки, некоторые из которых носят рефлексивный характер. Будем считать, что скрытие косвенных признаков невозможно.
Приведем определения для признаков распознавания. Введем обобщенное обозначение S для некоторой стратегии игрока.
Признак α называется необходимым признаком для распознавания стратегии, если он принимает значение истина всякий раз, когда реализуется распознаваемая стратегия. В символах математической логики это отображается импликацией S → а и правилом вывода (распознавания) S,S → α/α: если противник выбрал стратегию S, то должен наблюдаться признак α.
Признак β называется достаточным признаком для распознавания стратегии, если из факта наблюдения признака β (логическая формула признака приняла значение истина) следует выбор стратегии S. В символах математической логики это отображается импликацией β → S и правилом вывода (распознавания) β/β → S/S: если наблюдается признак β, то противник выбрал стратегию S.
Признак γ является необходимым и достаточным для распознавания стратегии S, если утверждения γ и S одновременно истинны или одновременно ложны. С прикладной точки зрения наблюдение признака γ позволяет делать безошибочный прогноз о выборе противника.
Из факта наблюдения признака α не следует достоверное заключение о выборе стратегии. Следует лишь возможность реализации распознаваемой стратегии S, поскольку множество истинности признака а шире, чем множество истинности необходимого и достаточного признака у. Однако, из факта ложности признака α (наблюдается ā ) следует, что стратегия S не будет реализована. Действительно, это следует из закона логики ( S → а) → ( а → S ). Из факта отсутствия признака β не следует, что стратегия S не будет реализована, поскольку множество истинности достаточного признака уже, чем множество истинности признака γ.
Читать дальше
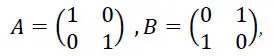
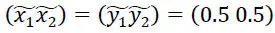 . Здесь введены обозначения: 𝑥 1, 𝑥 2– вероятности с которыми игрок 𝒜 выбирает первую (𝐴 1) или вторую (𝐴 2) стратегию (первую или вторую строчку матрицы 𝐴); аналогично (𝑦 1𝑦 2) – распределение вероятностей на стратегиях 𝐵 1,𝐵 2(столбцах матрицы 𝐵). Математическое ожидание выигрыша для игрока 𝒜 равно 0.5. Дополним описание данной игры допущением, что для каждой стратегии игроков известны признаки распознавания, известные обоим. Кроме того, для каждого такого признака существуют косвенные признаки, некоторые из которых носят рефлексивный характер. Будем считать, что скрытие косвенных признаков невозможно.
. Здесь введены обозначения: 𝑥 1, 𝑥 2– вероятности с которыми игрок 𝒜 выбирает первую (𝐴 1) или вторую (𝐴 2) стратегию (первую или вторую строчку матрицы 𝐴); аналогично (𝑦 1𝑦 2) – распределение вероятностей на стратегиях 𝐵 1,𝐵 2(столбцах матрицы 𝐵). Математическое ожидание выигрыша для игрока 𝒜 равно 0.5. Дополним описание данной игры допущением, что для каждой стратегии игроков известны признаки распознавания, известные обоим. Кроме того, для каждого такого признака существуют косвенные признаки, некоторые из которых носят рефлексивный характер. Будем считать, что скрытие косвенных признаков невозможно.










